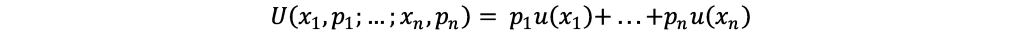Tag: Rational

Settling accounts with the losses

Why do we get so confused while selecting the best smartphone model and end up selecting high-costing ones? Why do people still fall for easy money schemes, Ponzi schemes, Pyramid schemes even though they are well informed about similar fraud cases? Why most of the people are ready to buy a million-dollar lottery ticket costing few pennies even when they know that the chances are very low? Why do people fall in the spiral of gambling even when they have hit the rock bottom of debts? Why retail investors are continuously losing huge amount of money in stock market when they know that it is a loss-making venture? What convinces them to continue further? Why people always lookout for complete cover while selecting insurance policies even when they know that chances of those problems are really low? Prospect theory has answers to these questions.
Daniel Kahneman and Amos Tversky’s Prospect theory shows certain behavioral effects called certainty effect, reflection effect and isolation effect while making economics related decisions. Prospect theory explains why people love certain but smaller gains and also why same people will turn into complete gamblers in a crisis situation.

Daniel Kahneman and Amos Tversky’s Prospect theory in economics

Prospect theory is one of the most important ideas of behavioral economics. It shows how people make choices when times are highly uncertain. Rationally, any person would go with the choices having the best probable outcomes in uncertain times but in real scenarios that is not the case. Real people are emotional and always have mindset of survival. That is exactly why in uncertain times, people choose anything that has complete surety, certainty of gain instead of gambling for higher gains however highly probable they may be. And when probable gains are very high than average gains people will choose higher gains even when they have very less probability. This irrational, non-economical behavior may make human decision seem illogical, inconsistent. This illogical behavior is an important part of our evolution as species which Nobel Laureate Daniel Kahneman’s Prospect theory highlights. We will throw more light on prospect theory hereon.       

Expected Utility Theory

“The agent of economic theory is rational, selfish, and his tastes do not change.”

Expected utility theory lies at the foundations of economics. It allows economists to model the scenarios to understand the dynamics between the resources, their perceived value and the risks/ uncertainties involved in any transaction.

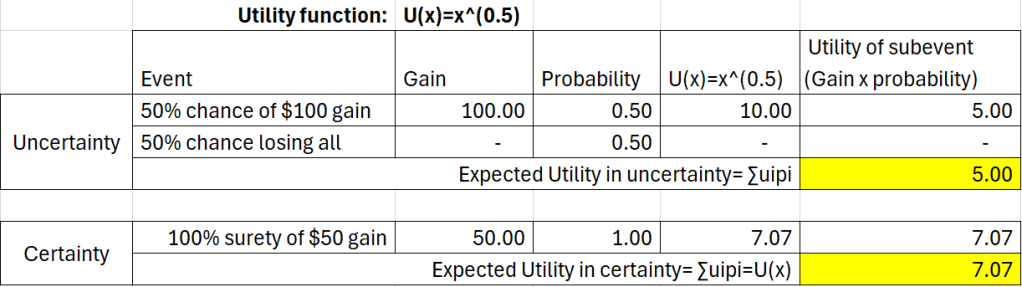
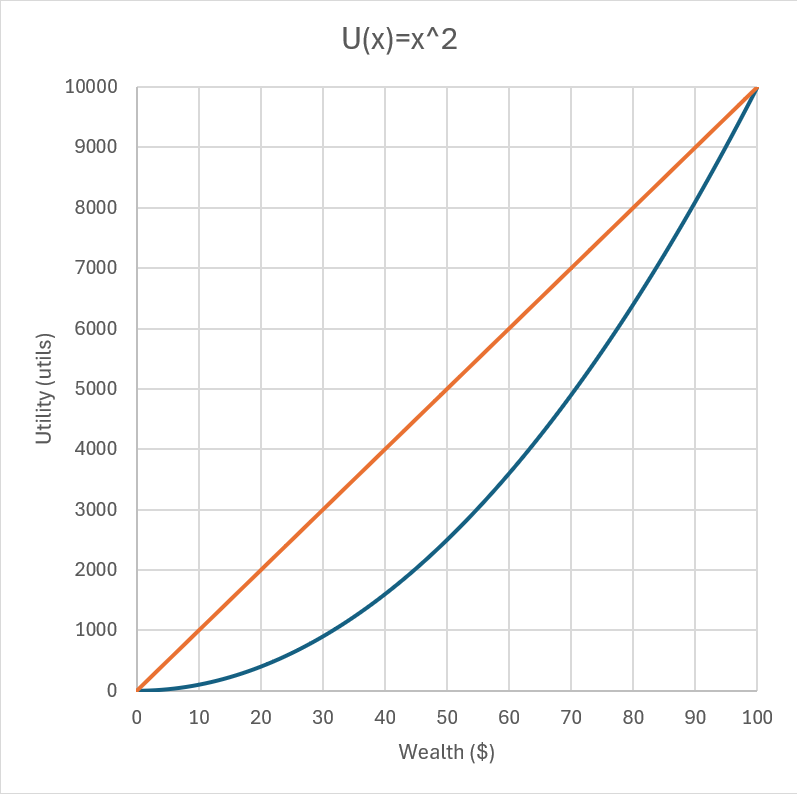
The basic idea behind expected utility theory is that for any given set of uncertain events, a rational agent considers the weighted average of all gains based on the probabilities. The rational agent makes decision based on overall gains rather than being biased towards certain high value gains or certain highly probable gains.

For those who want more details, I have written in depth on the expected utility theory.  

Prospect Theory

Although expected utility is one of the fundamental concepts of economics, the assumptions on which it stands have their own limitations. So, expected utility theory is not a complete and absolute theory to understand and predict the behavior of agents in economics. The moment we are injecting the word “behavior” we must understand that humans are not a purely mechanical or mathematical thinkers – decision makers. Also, as per the expected utility theory, there can be different perception of the value for given same resource for different agents. What expected utility immediately does is to fully attach the perception of value of given gain only with the bulk of resource that agent already has and the value addition it would do to this already existing bunch of resource. There is no psychological element in this discussion which is a larger predictor of the behavior of the agents in economics.

So, you can call prospect theory as an augmentation of expected utility theory. Prospect theory is not meant to falsify the expected utility theory rather it helps EUT to evolve where its own assumptions fail to explain the behavioral decision of the agents.

Modern economists are making more efforts to incorporate the psychological aspects of decision making into the machine-like purely mathematical models of economics. This makes the predictions more realistic when human decision making is involved. Daniel Kahneman and Amos Tversky published their world-famous paper called ‘Prospect theory: An analysis of decision under risk’ in ‘Econometrica’ in 1979. This paper is one of the most cited papers in economics. Prospect theory thus became the cornerstone of behavioral economics.

Kahneman and Tversky pointed out one “theoretical blindness” imparted due to the EUT. We will see those details in depth. They pointed out certain effects based on the decision making of the subjects under different decision-making events. Collection of these effects makes the prospect theory important. The important point to keep in mind is that everyone is risk averse in reality. Nobody wants to choose the transaction where there expected utility is reduced. So, the utility function of agents is concave. 

Certainty effect

People overweight outcomes that are considered certain, relative to outcomes which are merely probable.

According to EUT, people will weigh out the outcomes based on their probabilities, but Kahneman-Tversky found out that people love certainty of gains. People don’t want to get involved into gambles when they know that there another way to gain something “closely valuable” for sure.

Kahneman-Tversky presented an interesting observation in their paper, here are the exact scenarios:

Choose between

A:            Gain of 2500 with probability 0.33

                Gain of 2400 with probability 0.66

                Gain of 0 with probability 0.01

OR

B:            Gain of 2400 with certainty

According to the EUT the utility equivalent of A can be calculated as

U(A) = (2500 x 0.33) + (2400 x 0.66) + (0 x 0.01) = 2409

And utility equivalent of B

U(B) = (2400 x 1) =2400

So, according to EUT the utility of A is higher than B. But you already have your answer ready in your mind. Same was observed by Kahneman- Tversky; 82% of the people choose event B where the gain was certain.

Does this mean that the more probable the gain the more preferred it will be?

The answer is complicated.

Kahneman- Tversky further posed a modified event,

Choose between

C:            Gain of 2500 with probability 0.33

                Gain of 0 with probability 0.67

OR

D:            Gain of 2400 with probability 0.34

                Gain of 0 with probability 0.66

They observed that 83% of the people chose event C over event D. This was surprising because event D is mathematically more significant (probability of 0.34 in D over 0.33 in C). This shows that it’s not just about the higher certainty which drives the preferences. The moment given options are uncertain people rarely notice the extent of the uncertainty (numerical value of probability) to choose between.

Take one more example given by Kahneman-Tversky

A:            Gain of 4000 with probability 0.80

OR

B:            Gain of 3000 for sure

Here 80% of people chose B.

But when presented following:

C:            Gain of 4000 with probability 0.20

OR

D:            Gain of 3000 with probability 0.25

Here 65% people chose C.

What exactly is happening here?

People love sure gains over any uncertain gains. But when both or all of the presented gains are uncertain, people will choose to gamble with those giving higher gain, whatever may be the possibility. This goes against EUT which says rational people would consider both the gain and the probability while making a decision. In reality when people are uncertain, they choose to go with the uncertain but higher chances of gaining.

You will now start to notice that EUT creates an objectivity in the choices by mathematically connecting the gains with their probability. But Kahneman-Tversky observed that real people will not follow EUT, they will make decisions based on the prospects they are presented. People never look at the scenarios in economics as distinct events, they look at the current trade-offs, current prospects they a have at their disposal to choose. The choice is always relative to the prospects presented and not absolute like EUT asks for in a mathematical form. That is exactly why Prospect Theory becomes important. It’s neither about the certainty nor the value, its more about what type of options – prospects you are providing to the people.

This is one important idea in marketing. We will see that in detail as the discussion evolves.

There is an interesting observation by Kahneman-Tversky when we are observing relativity of the prospects:

Choose between

A:            Gain of 6000 with probability of 0.45

OR

B:            Gain of 3000 with probability of 0.90

86% of the people chose prospect B.

If you use EUT, both prospects have same utility equivalent = (6000 x 0.45) = (3000 x 0.9) = 2700.

But people refuse to be indifferent to these prospects and choose the most certain prospect.

Now, one more – same gains but totally different probabilities,

Choose between

A:            Gain of 6000 with probability of 0.001

OR

B:            Gain of 3000 with probability of 0.002

Here, 73% of the people chose prospect A.

Again, both have same utility equivalent = (6000 x 0.001) = (3000 x 0.002) = 6. According to EUT people should be indifferent to both prospects.

And interestingly they didn’t go with the one which is more certain than other. They went the one with larger gain. This is because both prospects have very slim chances of gains.

Now it should be pretty clear that people compare prospects based on what is presented to them. Even when they are risk aversive, they would prefer bigger gambles when they realize that the chances of winning are really low and there is pretty much nothing to lose.

Reflection Effect

The risk aversion in the positive domain is accompanied by risk seeking in the negative domain

Certainty increases the aversiveness of losses as well as desirability of gains.

We saw how people choose when they have information of higher certainty or higher gains. What would happen if we inform them about lower certainty or lower gains/ higher losses?

We already saw one observation from Kahneman-Tversky:

A:            Gain of 4000 with probability 0.80

OR

B:            Gain of 3000 for sure

80% of people chose B because they preferred surety of gain.

Kahneman-Tversky posed exact negative of this prospect which looks like

A:            Loss of 4000 with probability 0.80

OR

B:            Loss of 3000 for sure

Now, 92% of the people chose option A. They don’t want a prospect where loss is certain.

Kahneman-Tversky observed that when prospects are negated people switched sides. The risk aversion in positive prospects changed to risk seeking which goes against EUT. They called it the reflection effect.

See this already discussed prospect:

Choose between

A:            Gain of 6000 with probability of 0.001

OR

B:            Gain of 3000 with probability of  

73% of the people chose prospect A.

The negative of this would be:

Choose between

A:            Loss of 6000 with probability of 0.001

OR

B:            Loss of 3000 with probability of 0.002

Kahneman-Tversky observed that 70% of the people chose prospect B.

When it came to losses, people chose prospect with more certainty of lower loss.

This is very interesting observation. If you still cannot wrap your mind around this, the simplification looks like this: People rarely care about the combined effect of gains/losses with the probabilities as the expected utility theory rationally establishes. People care about what current choices they have and choose those which guarantee highly certain gains even when they are low and choose lower losses when they are highly certain.

“…it appears that certainty increases the aversiveness of losses as well as the desirability of gains”   

Isolation effect

In order to simplify the choices between alternatives, people often disregard components that the alternatives share, and focus on the components that distinguish them.

The core of this idea is that people don’t like complexity or our brain is always trying to take shortcuts. This is one important idea and observation on human nature which Kahneman-Tversky pointed out.

What they did is creating a two-stage game:

 1st Stage-

P:            Gain of 0 with probability of 0.75

OR

Q:           Move to 2nd stage of the game with probability of 0.25

2nd Stage-

R:            Gain of 4000 with probability of 0.8

OR

S:            Gain of 3000 for certainty

The condition here is that choices must be made before the game is played i.e., before the actual outcome becomes apparent.

  Before we go to what Kahneman-Tversky observed. Let us see what EUT would prefer, what a rational person would prefer:

U(R) = The equivalent utility of gaining 4000 at the end of the game = 4000 x (probability of reaching 2nd stage from 1st stage) x (probability of gain of 4000) = 4000 x 0.25 x 0.8 = 800

U(S) = The equivalent utility of gaining 3000 at the end of the game = 3000 x (probability of reaching 2nd stage from 1st stage) x (probability of gain of 3000) = 3000 x 0.25 x 1 = 750

So, U(R) > U(S). Thus, any rational person would choose prospect R in any situation as per the EUT goes.

Pay attention here,

The added complexity due to multiple stages –

When people were presented with the above mentioned two stage scenarios, 78% of the people chose the prospect giving certain gain i.e., gain of 3000 for sure. But, according to EUT you will see that this chosen prospect has lover equivalent utility. People actually ignored (or didn’t account for) the effect of the first stage of probability which would allow them to enter the actual stage 2.

Kahneman-Tversky called this an Isolation effect where people isolate or don’t care the commonalities between presented scenarios to make the decision-making process less complicated.

Now, this 2-stage game can be reduced to single stage game as follows:

Choose between

A:            Coming to current stage with 0.25 chance where there is 0.8 chance to gain 4000

                (0.25 x 0.8) chance to gain 4000

Gain of 4000 with probability of 0.20

OR

B:            Coming to current stage with 0.25 chance where there is certainty to gain 3000

                (0.25 x 1) chance to gain 3000

Gain of 3000 with probability of 0.25

This is a reduced form of the prospect.

If EUT is applied here

U(A) = 4000 x 0.20 = 800 and U(B) = 3000 x 0.25 = 750.

The 2-stage game and its reduced form obviously will have exactly same equivalent utilities because the reduced form just combines the chances of two stages into one resultant number. So, even though these two scenarios have same outcomes of equivalent utilities, Kahneman- Tversky observed that the ways in which these scenarios are presented affect the choices of the people.

Kahneman-Tversky had already observed that when there is significantly less difference in the amounts of gains or the probability of those respective gains in two prospects, people mostly prefer the one with higher gains. So, if we present this above mentioned 2-stage scenario to its reduced single stage scenario the results are interesting. 

We have already seen what Kahneman-Tversky observed for this reduced scenario. Majority of people chose higher gain prospect even though it was relatively less probable.

Conclusion

What Kahneman-Tversky did concretely in prospect theory is to formulate the value function to mathematically explain this behavior.

The value function in prospect theory is given as follows:

The simplified idea of this value function is:

The pain of losing certain amount hurts us more that the joy of gaining the same amount.   

You just like winning and dislike losing – and you almost certainly dislike losing more than you like winning.

The importance of prospect theory is that it shows what it means to be a human. Once you start collecting the pieces of certainty effect, reflection effect and isolation effect the picture that is revealed is profound insight about our tendencies to ensure survival in any case.

Certainty effect shows that people will choose certain gains even if their size is low. They just want to be at peace with increasing their existing surplus if it is sure.

This is how the coupon codes, vouchers, discount codes, discount days work in online shopping. The provider lures you into buying something you really don’t want by giving you guarantee, surety that you surely are making profit out of this deal. One smart thing that happens here is that the sense of urgency. You might have realized that these coupons are expiring immediately like virtually now. This creates an urgency to materialize the profit.

When people are in profit making environment, they will always prefer sure profit over uncertain profits and that is exactly how scammers lure people. They create this sense of surety to attract people to invest in their schemes.

No wonder why people love easy money. Once you inject the surety of gains in any venture people will literally pile up and that is how Ponzi schemes, Pyramid schemes work.     

The moment this surety of gain is lost and when people realize that it is only the losses that they will have to face then immediately this same population craves for uncertainty in the losses. When people see that they anyways have to digest the losses they avoid certain losses over uncertain ones, even if the actual effect of certain losses was pretty low. This is reflection effect.

The stock market is the best example to explain the reflection effect. In the crisis times – bearish markets, history has evidences that people have gone with insanely foolish bets where chances of gains are slim to none. People end up in the cycles of betting, gambling even when the realistic indicators of market are pointing to inevitable crisis.

The important thing to appreciate from prospect theory is to know when and where to stop in crisis situations.

“…people become risk seeking when all their options are bad”

If you have lost this game in poker or any gamble, you always feel that I will play the next game and definitely (somehow) will recover my losses (even when I know that James Bond is sitting on my table).

You will be more relaxed if you were told in advance that you will make less money of $10000 and you will be more stressed, feel pain if you make $12000 and government cuts $2000 for some taxation at the last moment. The gain is same but the “prospects” are different.

People can be confused to choose the loss-making options even when they are completely informed. When decision making is multi-stage so that there are some common things between them, people usually neglect those shared attributes even if they are significant and move on to the differences to finalize the choice even if these differences are not significant. This is isolation effect.

Many electronics companies while creating their pricing strategies intentionally create shared features and smartly just add one low-cost additional feature in the top model to sell it at foolishly, unjustifiably higher cost. People are ready to pay higher prices for that low cost (for the manufacturer/ marketeer) because it makes that model better. (You know who I am talking about.)

For me, the isolation effect has a huge philosophical implication.

Kahneman-Tversky have attributed the behaviors pointed out by Prospect theory to the tendency for survival. If you want to survive and are living in an already good situation then you would not want to disturb the current resources you have, that is why you don’t prefer uncertain gains, you are more than happy if the gains are certain even if they are small in size because they are not disturbing the already materialized gains.

In same way when conditions to survive are hostile you would take that every chance to increase your resources, however slim the chances may be. This is some kind of indication of hope. Important thing about Prospect theory is that Kahneman-Tversky pointed out that this exact risk-taking tendency in negative environment can push people into the spiral of continuous losses.    

We are naturally evolved in this way. 

The isolation effect outlines our tendency to eliminate common/ shared attributes of given resource to make a choice. The key thing to appreciate here is that while neglecting these commonalities we are never conscious of how significant they are in our life. You must appreciate that when I am writing this, sharing this, when you are reading this, we have more than enough resources to sustain a basic life. We are living better life than most of the world population but still we are not satisfied because we have already isolated that which we have with us. The isolation effect thus points out to our tendency to lose the feeling of gratitude for everything we have right now.

We rarely appreciate things which we already have or things we are sure that we would never loose. Many times, people realize the worth of things as really significant – as truly valuable when they are lost. 

Being alive and having the ability to experience – to appreciate this life is what common to all of us, this is precious than anything else in this world, rest is just the bonus. We should not let the practice of comparison isolate this preciousness.

References and further reading:

  1. Kahneman, Daniel., and Amos Tversky. “Prospect theory: An analysis of decision under risk.” Econometrica 47.2 (1979): 363-391
  2. Thinking fast and slow – Daniel Kahneman
  3. Risk and Rationality in Uncertainty – On Expected Utility Theory
  4. Connecting money with sentiments – Behavioral Economics

Risk and Rationality in Uncertainty

We have many philosophical ideas about how money is not everything in life but deep down, everyone knows how money constitutes to a bigger portion of who we are. Although money can’t buy everything, the unexplainable value it holds behind presence of almost everything in our lives will never go unnoticed. We know that this importance of money/ resources/ assets is highly dependent on how much of those we have right now and how much of those may get lost in an uncertain event. This perception of value drives our decision making in risky situations. The Expected Utility Theory (EUT) in economics deals with the modelling of such scenarios. The mathematical formalization of the perception of wealth and our risk profile is facilitated by this fundamental theory. EUT lies at the foundation of actuarial science/ insurance, financial risk management, decision making under budget restrictions, asset management, and investment management.

EXPECTED UTILITY THEORY

We live in an uncertain world. Timing events where too many interactions are happening could be risky especially when it comes to money or the basic resources for sustenance. In crisis situations, our survival instincts have always kicked in to ensure preservation of life and the resources required to ensure its longevity. They need not to be always rational, they are just meant to save life somehow, that is why most of the acts of survival seem extraordinary. Interesting thing to understand here is that when such extraordinary survival instincts kick in as a mass effect the whole mass effect becomes irrational, unexplainable, incoherent. There is no sane explanation to justify these mass events. When such events badly affect the resources responsible for basic life of every being, it can be catastrophic. Huge sudden falls in stock market are good indicators of such disasters, crises. Insurance on the other hand could prepare person to handle the disasters in a preventive way. Stock market and insurance are one of the best examples to understand how people assess risk and maintain/ reject rationality while making important decisions. We will see what formal ideas from economics lie behind these events of uncertainty.

Expected Utility Theory (EUT) in Economics

Expected utility theory lays the foundation of how a rational person would make decision in an uncertainty where valuable resources like money are involved. The whole idea is based on the quantification of that uncertainty and connecting that uncertainty with the individual gains from individual uncertain event. Expected utility also creates a formal structure of how person perceives risk in given scenario. This helps to quantify the value generated from any economic event.

Origin – St. Petersburg Paradox

Daniel Bernoulli is credited to establish the expected utility theory which is one of the foundations of economics. The theory emerged from the St. Petersburg Paradox which goes like this:

You have $2 and we toss a coin. Heads, the amount you have now is doubled and tails then the game stops and you leave with whatever amount you have right now. The game continues till its always heads in series and stops when the coin shows tails.

The question is how much will you be willing to pay to enter this bet?

The probability of heads and tails is 50-50% which is ½ . If it is a series of heads (heads followed by heads) then the events are dependent on each other, so the probability of this event is intertwined with the probability of the previous one. If there happens a game where you start with $2 and every time heads comes, and the money goes on doubling the equation of gain would be:

As this math goes, a person should pay infinite amount as he will be gaining infinite amount from such game. ‘E’ value here is identified as expected value. Even if one such possible game would happen in reality, people won’t pay infinite amount in reality to enter this bet. 

Bernoulli resolved this paradox by creating the concept of Expected utility. People will pay not what actual value it delivers (as in the $s of money); they will pay according to how actually it will be useful to them, ‘utilizable’ to them – that is where the utility and thus expected utility comes in picture.

Expected utility is calculated by the amount one would gain and the chances of gaining that amount. The expected utility thus is sum of all the gains connected with the probabilities of gaining them.

Daniel Bernoulli
The determination of the value of an item must not be based on its price, but rather on the utility it yields.

1st Tenet of EUT: Expectation

The overall utility of a prospect, is the expected utility of its outcomes.

In very simple words, for a given scenario you will weigh the chances of its constituent events and connect them with their respective gains. The sum of the all connections of each gain with their chance of realization is the usefulness – utility of that scenario.

Mathematically,

Expectation:

In our example we need to assume something that is the usability of the money – utility.

We assume $10 has utility of 1 unit. (This is just an assumption to understand the concept. When multiple objects are involved, their utilities will be different.)

So, the expected utility of this scenario is:

E = ((1000/10)x0.2) + ((50/10)x0.65) + (10000)x0.15) =

20 + 3.25 + 150 = 173.25 units

So, the expected utility – the usefulness of this event is 173.25 units.

The unit of value which we assumed in this calculation is sometimes called ‘utils’ – the basic unit of utility. It will change based on how one perceives the value in given scenario. 

You will realize that the expected utility is the weighted average of utility of events and their individual probabilities.

Four Axioms of Utility Theory

Later John von Neumann and Oskar Morgenstern expanded the concept of EUT with the idea of rationality. The agents involved in such uncertain economic exchanges are ‘econs’-the rational beings.

Oskar Morgenstern & John von Neumann

They have clear preferences among the options provided in every economic decision which comes under the idea of “completeness”. If out of the given set they select multiple options at a time, then it is said that they are ‘indifferent’ to these options. Whatever might be the internal distribution of constituent they might have. It’s about the final utility they perceive. When presented with choices, a rational person has clear preferences for those choices.

For all given uncertain events there is a hierarchy of preferences. If A is preferred over B and B is preferred over C, then A is always preferred over C. Which goes as transitivity.

Suppose we have been presented three events where event A is preferred over B and B is preferred over C. Now if one introduces a new event N which is slightly less preferred than B and more preferred over C then event B and N would be indifferent. In simple words, the choices between options would never directly jump, they will align as per the preferences in line.

So, A>B>C and B>N>C then A>B>C and A>N>C mean the same.

This is continuity. Graphically, the utility function is always a smooth curve.

Why do A>B>C and A>N>C mean the same even when the calculated numeric value would differ? It is because utility is never an absolute value it is just used to arrange the preferences by quantifying them. Ground rules used to define usability from the given resources i.e., the utility function of given scenario will be different for different scenarios and different sets of people. This is simplification of the concept called ordinality of utility. You can rank utility but not say that event A is this many percent better than event B.

When you have set the preferences of A over B and if you are offered another totally different/ irrelevant event M with new utility. You would still prefer A over B. Introduction of M will not affect the preferences as if A and B are independent of M. This is called ‘independence‘ in EUT.

So, completeness, transitivity, continuity and independence are the four axioms of EUT. Note that they are not ‘complete’ representation of reality. It’s just that they bring in simplicity to treat given scenarios and evaluate them. That is why you will find contradictions to these axioms. (Maybe a topic for another time.) The axioms are there to create a formal mathematical structure to draw useful inferences.  

2nd Tenet of Expected Utility Theory: Asset Integration

In EUT, asset integration is an idea based on the assumption that all people making economic decisions are rational. So, in uncertainty or risky scenarios a rational person will look at the overall gains instead of focusing on one certain gain and neglecting other unsure gains. A rational person will look at the risks of scenarios in a collective way and decide to enter only if the expected utility improves his assets’ position. A rational person will only enter the given scenario if the collective utility is better than the individual utility of its sub-events or sub-gains.

A rational person will not focus on an individual more probable gain even when his overall gains are becoming low.  

3rd Tenet of Expected Utility Theory: Risk

The beautiful insight EUT creates is about the mathematical formalization of risk profile. For that we will understand some ideas in advance.

Utility function – it is a mathematical relation between how one sees the value of given object/ resource. The value of resources is different for different people. A crude example would be how a beggar values money for one time meal compared to a filthy rich person. The value of $25 would be different for different people based on the conditions they are in.

This is where marginal utility comes in picture.

Marginal utility talks about what difference it makes in your perception of the value of a given thing if one would give you more of that in the next event. Roughly speaking the more we have something, the less we value it, so marginal utility is always diminishing. If I already have 10 packets of chocolates which are enough for the day to me, the next 11th packet of chocolate won’t make that much difference in my current excitement of having 10 packets. (Please note that we are talking about rationality here, although nobody is rational when it comes to chocolates.) A rational version of me would trade that 11th packet for something else with a person who hasn’t received even a single packet. A person who has no chocolate would perceive that single packet with higher value than how I perceived it (provided that he loves chocolates).

Alfred Marshall – the British Economist brought the concept of
‘Marginal Utility’ through his book ‘Principles of Economics’ in 1890.

So, utility function is a mathematical transformation of objects in given event to a unitary value so that the results can be easily compared with each other because the transformation converts everything to single unit system. These single unit of value is called ‘util’.

Utility function can be any possible mathematical relation. Generally, it is expected to be simple to not invite the complexities in modeling of given economic scenario. It should be simple enough to draw realistic conclusions.

An understanding of utility function gives insight into how the person evaluates risk with respect to the resources they hold.

Consider a scenario:

Event 1 – You enter a lottery where there is 50% chance that you will win $100 and 50% chance that you win nothing.

Event 2 – You are given $50 for sure, unconditionally just for playing the lottery.

Assume we have three differently thinking people to make choices in this scenario. Different thinking means how they assess the risk of entering the lottery which has some uncertainty and the surety of winning $50. Difference in assessment of risk means difference in the perception of utility. It further means that the utility function will be characteristic to each person.

Person 1 has the following utility function:

So, for Person 1 the utility of certainty (7.07 utils) is higher than the uncertainty (5 utils). He is happy to walk away with sure $50 gain instead of betting for $100 lottery.

Person 1 doesn’t want to take risk by entering the Event 1 of betting when he is sure about gain of $50 in Event 2. This is risk-averse behavior. The utility function mathematically models that risk averse behavior. Utility function is concave in risk aversion.

Now comes Person 2 with the following utility function:

You will see that the utility of certain and uncertain choices is the same. It means that it doesn’t matter for this guy if he enters the lottery having uncertainty or gets $50 for sure. This is risk-neutral behavior. The person 2 doesn’t care about certainty or uncertainty. He values both events the same. As mathematically both have similar utilities. Person 2 is indifferent to both events.

Now see the Person 3 with following utility function:

This guy has a radical view, he perceives the worth of entering the lottery (5000 utils) better than gaining $50 for sure (2500 utils). This guy is gambler! He finds it more interesting to enter the bet instead of gaining $50 for sure. He is happy to take the risk in uncertainty.

Looking at these three people you should note that the scenarios/ events they are presented are exactly the same. The only thing which is different is how they see the value in lottery and the sure gain.

So, the first person demonstrates risk averse behavior. He wants surety of gain rather than gambling for higher but unsure gain.

The second person demonstrates risk neutral behavior. Bet or no bet he doesn’t care. Just be done with it.

The third person demonstrates risk loving behavior. He wants the thrill of uncertainty in betting, so he sees more value in uncertainty of lottery.

This is how Expected Utility Theory can be implemented to mathematically model how different sets of people/fund managers will make decisions based on the risk profile. The relation between expected utility (which is the weighted average of gains) and utility function (which shows how one values the gain) can show us the risk profile.

Risk Averse Utility Function
Risk Neutral Utility Function
Risk Loving Utility Function

In the graphs shown, blue lines show utility function and the orange lines show expected utility. The orange line in our case connects the utility of $100 and $0 which is Event 1. This orange line connects any points on utility curve and it will give the expected utility value for that scenario of uncertain gain. In simple words, it’s the line of weighted average exactly like the definition of expected utility. This line is used to find out the certainty equivalent (CE). A certainty equivalent is the utility of an uncertain gain if it was certain.  

Almost all the time, people are risk averse. People want to avoid uncertainty about higher gains when they are presented with some lower but sure gain. This is where marginal utility becomes important. (This point deserves broad explanation which we will cover another time under Prospect Theory)

Marginal Utility

In risk averse people, you will see that the utility function starts to flatten out once the value gained increases. The more value someone already has the less he values the next addition of bunch into the preexisting bulk. Remember the chocolate box example?

One with 10 boxes of chocolate perceives one additional box with less value, whereas some with no chocolate will see it as a precious one as he has nothing right now. The perceived value of the additional next lot goes on reducing. This is known as diminishing marginal utility. Marginal utility is always diminishing.

So, a safe playing person would stop entering the next gamble because he now has enough. The next uncertainty in gambling has less value for him.

EUT in actuarial

Now it is obvious that only a risk averse person would go for conservative approach in uncertainty. This also means that risk aversion will also invite preventive measure against loss of certain assets, resources. Insurance thus comes into the picture. EUT here helps to mathematically formalize the probability of the risks which would compromise current gains, the perceived value of asset/ property/ resource and losses one can bear. We can now calculate the premium for the insurance against uncertainty of loss of something.

So, we will look into a scenario where risk aversion exists thus marginal utility is always diminishing.

We have the utility function of a man has a property giving revenue of $100K/year as:

u(x)=ln x

Now will see the risk scenario. Suppose this person does a fire audit of his property and the auditing agency finds out that there is 50% chance that he will suffer a loss of $60K/year due to fire hazard and 50% chance that nothing will happen.

After rephrasing, the gains from the property would look this:

50% chance that the income is $40K/year and 50% chance that income is $100K/ year.

Using the tenets of EUT the mathematical expression becomes:

Now, what we are doing differently here is to find out what this expected utility in uncertainty means when there is complete effect of loss with some chance and gain of some chance. In earlier examples we had second event of certainty against which we compared to understand the risk profile. Now it’s reverse calculation, we know the risk profile, we know the perceived overall value i.e., EUT of the property. Now we will find the certainty equivalent (CE) using the risk profile which can be explained by the utility function of the person.

How much is this 11.05 utils in terms of money from the property for this guy? We can find this from utility function of the person.

ln(x)=11.05, thus x=$63245.55

Now, think the fire hazard as a lottery where you gain $63245.55 money as per EUT calculation. Whether the fire will happen or not, the possible overall earning from this property would be $63245.55.

Now, if the property without any fire hazard was giving me $100k and the insurer guarantees me that same earning for the losses due to hazard. How much maximum amount should I pay to the insurance agency?

I will pay only that much amount which falls short to the $100k when compared to perceived earning calculated from the combined effect of certainty and uncertainty as given by EUT.

My earing due to uncertainty is $63.2k/year, I would receive $100 for a fine year so in order to continue that $100k even for a worse year I would pay insurance agency = $100000 – $63245 = $36754.45.

Anything I am paying above $36754.45/ year for insurance premium is loss for me. I would not go above this amount to insure my property which guarantees income of $100k per year. This is how the insurance premium is decided.

Conclusion:

We have many philosophical ideas about how money is not everything in life but deep down everyone knows that money constitutes a bigger portion of who we are. Although money can’t buy everything, the unexplainable value it holds behind presence of almost everything in our lives will never go unnoticed. We know that this importance of money/ resources/ assets is highly dependent on how much of these we have right now and how much of those may get lost. This perception of value drives our decision making in risky situations. The mathematical formalization of the perception of wealth, our risk profile is facilitated by expected utility theory. Although this theory has its own limitations it lies at the foundation of the economics.

For further reading:

  1. Von Neumann, John, and Oskar Morgenstern. “Theory of games and economic behavior: 60th anniversary commemorative edition.” Theory of games and economic behavior. Princeton university press, 2007
  2. Kahneman, Daniel., and Amos Tversky. “Prospect theory: An analysis of decision under risk.” Econometrica 47.2 (1979): 363-391
  3. Thinking fast and slow – Daniel Kahneman
  4. Connecting money with sentiments – Behavioral Economics
  5. Settling accounts with the losses – On Prospect Theory

Game Theory – Minding our decisions

“All stable processes we shall predict.

All unstable processes we shall control.”

– Jon von Neumann

Human relationships are more of multiple complex interactions. The interactions with living or non-living bodies create some actions and these actions have some favorable or unfavorable outcomes. The word “relationship” here is not used just as in parents, siblings, in-laws or acquaintances but as a connection to everything around us, mostly living things. The awareness of our actions and their consequences- that visualization of cascade is one of the major parts of our knowledge building, relationship development, behavior management, personality development.

As a sane creature (most of the time) we try to calculate the consequences of our actions, have a thought about it and then decide our strategy while acting on something. This is what some people call the motivation or habit or trait of that person, that character. Important thing to understand is that every action always has multiple outcomes which brings the complexity in the expected outcomes of the scenarios. Different people have different motivations/ habits/ traits so they react and decide in different way adding further complexity to the scenario.

Take a simple example:

Many a times when you are trying to call your friend this happens. You call him, his phone rings but he doesn’t pick up. Then he notices the missed call and tries to call you while you are already calling him. The call remains engaged from both sides. Then you both wait for exactly the same time oping that the one on other side will call.

This goes for some time, and after some trial and error your call gets connected.

What should be an optimal strategy for such simple scenarios?

There is a rigorous field of mathematics and economics (not limited to these only and rather a wide field) which can deal with such problems and far more complex problems in our day-to-day interactions.

“Game theory is the study of mathematical models of strategic interactions among rational agents.”

 Simply put, game theory can give answers to have the best strategy for the interactions which can be business interactions, economical interactions, national interactions, war strategies or competitor strategies. The idea of Game theory was developed by famous mathematician Jon von Neumann and economist Osker Morgenstern. Let us dive in deeper.

Basic Definitions in Game Theory

Game– A game is any situation in which players (the participants- the agents) make strategic decisions—i.e., decisions that take into account each other’s actions and responses.

Agents– The participants, the players of the game.

Rational Agents– This is the most important idea in Game theory where the rationality of agent is the idea of welfare of the agent. The agent will always try to achieve its own welfare. In economics this is known as maximizing the utility.

A rational agent always tries to maximize its utility.

Strategy– Rule or plan of action for playing the game.

Payoff/ Outcome– The value of utility, extent of welfare from certain strategy. It is numerical, quantified measure of the benefit from a strategy.

Optimal Strategy– A strategy which maximizes the utility of an agent.

Please note that the clear definition of utility, rational agent, optimal strategy defines the boundaries of the problems in Game theory thereby making it mold-able into the mathematical models (although mathematical models can consider the factors beyond boundaries but it will make the problem unnecessarily complicated). Mathematical models as in the mathematical equations which can be solved using general techniques to get the maximized outcome for the agents.

Please note that the word “Game” in game theory can be any situation which requires strategic decision making involving more than one agent. The game can be simple like Stone-Paper-Scissors, Tic-Tac-Toe or a Chess game to more complex game like launching a new smart phone in the market or taking over a company or setting up a war with a nation or even winning the general elections of the country.

The Prisoner’s Dilemma

The Prisoner’s Dilemma is the most common and famous example to understand the basics of Game Theory. Consider a scenario:

Two persons are arrested by Police under the crime of armed robbery. The Police know that they have committed this robbery together but they don’t have enough proof to justify that. They can only charge the persons under the theft of the car used for robbery due to lack of evidences. Police think that if both persons confess the armed robbery, then they can easily jail them under the proper charges of armed robbery. So, they lock each of them in separate cell and ask them to either confess or deny the crime.

The police inspector tells each one of them separately in their cell the following:

If only one of you confesses the crime and the other doesn’t, then the one who confesses will be freed but the another one refusing will be sentenced for 10 years. If you both confess, you’ll each get 5 years. If neither of you confess, then you’ll each get two years for the car theft.

Now, if we see the overall scenario, the best thing for both the prisoners is to deny the crime and set themselves free at first, but if you think properly of all the consequences and the information available to both the prisoners, that is not the best strategy.

The common information of three possible cases given to both the prisoners by the policeman is known as Information Set in Game theory.

So, the outcomes of such scenario can be arranged in a table to form a matrix which is also known as the Normal Form in game theory.

If we assign a number to each the payoff of each strategy,

  1. 0 for the worst case- 10 years of jail
  2. 2 for 5 years of jail
  3. 3 for 2 years of jail
  4. 4 for becoming free, no jail

then the normal form can be given as follows:

Decision Matrix

 It becomes very easy to see as an agent of this game- the prisoner will try to maximize his utility by refusing the crime thereby setting him free. But the catch here is that he doesn’t know what another prisoner has done- whether he confessed or refused the crime.

Now, we need to understand that the final outcome is not dependent on only one prisoner decision. Hence, the decision making of second prisoner will affect the decision making of first prisoner. Let us see from the perspective of Prisoner 1:

  1. Refusing should be the best idea, but if Prisoner 1 refuses and the Prisoner 2 confesses then it will lead to 10 years of imprisonment (zero utility) for Player 1 more risky operation as he is not sure about Prisoner 2’s decision.
  2. If Prisoner 1 confesses the crime, then there are two possibilities:
    • Prisoner 2 also confesses thereby both will get 5 years of sentence (utility of two)
    • Prisoner 2 denies thereby prisoner 1 getting freed and Prisoner 2 gets sentenced for 10 years (utility of 4 for prisoner 1 and zero for prisoner 2)

 So, confessing becomes the best strategy for both the prisoners when they are in an isolated cell.

Which is why the optimal strategy for both the prisoners of this game is to confess. In any possible decision by another prisoner, it will give the best possible outcome.

The one thing important to notice here is that they both could have refused simultaneously. Because, if they both refuse it would have maximized the utility of both (2 years of jail for both, utility of 3 for both). The thing is that the risk associated with refusing is more than the risk associated with confessing. Thus, even if the utility is highest in some cases the interaction of other players forces a player to choose optimal strategy which will yield the best irrespective of other players decisions.

The Nash Equilibrium

Mathematician John Nash took the Game theory developed by Neumann and Morgenstern and provided mathematical background for finding the strategy where the solution will be optimal irrespective of the decision made by the other players. For that we need to understand the two types of games – Cooperative and non-cooperative games

If the prisoners in above examples are supposed to have a word with each other before presenting their opinion to the police they surely would have understood that refusing will benefit them both, which when exploited is a collusion – a foul play, here in the prisoner’s game it is exploited.

But as we know in reality, even if they are given a meet to discuss before presenting their opinion there is still that risk of changing the statement at the last minute (!) thereby making the game a non-cooperative game. Nash Equilibrium exists in such non-cooperative games.

A cooperative game represents the game where players agree to work towards a common goal. It’s like splitting your restaurant bill with your friends. Here the main focus remains on the contribution from each player, like Coalition of Countries to reduce carbon footprint, to stop Global Warming. Shapley value is used in cooperative games instead of Nash Equilibrium. Shapley value distributes the payoff based on the contribution a player makes in the game.

Shapley value simply decides the fairness of payoff for each player in cooperative game whereas Nash equilibrium decides the best decision to maximize the payoff in a non-cooperative game.   

“In non-cooperative games there exists an equilibrium at which no side has any rational incentive to change the chosen strategy even after running through all the choices available to the opponent”

In short, Nash Equilibrium is like a law which needs no punishment to enforce to the rational people, because the people understand that breaking that law will not benefit them.

It is like following a traffic signal properly. If all will rush at the crossing all will be late in their journey maybe possible deaths due to accidents. Following the time-based signal will give opportunity to everyone, thereby zeroing the risk of accidents and saving the travel time. (And still some people break the signal, hence the word “rational agent” is of highest importance in Game theory!)

John Nash – a mathematician received Nobel Prize in economics for his work of Nash Equilibrium. The development of mathematical tools further for game theory revolutionized the economics. The movie on his life called “A Beautiful Mind” depicts his original thought process in a beautiful way.

“I can observe the game theory is applied very much in economics. Generally, it would be wise to get into the mathematics as much as seems reasonable because the economists who use more mathematics are somehow more respected than those who use less. That’s the trend.”

– John Forbes Nash Jr.

Assumptions of Game Theory

  1. All players are utility maximizing rational agents that have full information about the games, rules and the outcomes/ payoffs. (So that the mathematical models will fit)
  2. Players are not allowed to communicate – no coalition in a bad way – no collusion- no foul play (hence the reason Governments also establish anti-collusion, antitrust laws, anti-monopoly laws in real world)
  3. Possible outcomes are known in advance and cannot be changed (Deterministic models, hence the reason many equity traders try to find some trends in the equity indices based on certain assumptions)
  4. The number of players can be infinite but most of the games will contextualize in terms of two players only (thereby simplifying the model).

Strategies of Game theory

  1. Pure and mixed strategies:
    • PURE- Players follow same strategy in the game- All the companies may increase the product prices of their products to increase the profit. (Actually, it not that simple)
    • MIXED- Different players follow different strategy in the game. (One company will try to sell less but expensive units, the another one will try to market the best-in-class after-sales services) 
  2. Dominant and dominated strategies:
    • A dominant strategy leads to the best of all alternative payoffs
    • a dominated strategy leads to the worst of all alternative payoffs
    • Say, there are two companies A and B both have two products – consumer and professional. The market has 80 % of consumers and 20 % of professionals. What can A and B do.
    • Company A and B both will enter both the consumer and professional market hence each will get 50% of the share from total market (half of consumer i.e., 40% consumer and half of professional i.e., 10% of professional market to each company), thereby maximizing the utility which is Dominant Strategy
    • Company A and B both will enter only professional market (which is already 20% of whole market- smaller market share) so both will get only 10% each of the total market thereby getting the least amount of market share which is Dominated strategy
    • Only company A can enter in consumer market and company B can enter professional market thus one will get complete consumer market and the another will get complete professional market. Reverse is also possible here.
    • The example i) here is called as Strictly Dominant Strategy, example ii) is called as Strictly Dominated strategy.
  3. Maximin strategy – A strategy which will maximize the profit, the utility in the game
  4. Minimax strategy- A strategy which will minimize the loss in the game

Game Theory for Life- The Concept of Finite and Infinite Game

The applications of Game theory are uncountable in real world. The complexity of real-life problems projects an impression as if Game theory has just started developing like a new born baby. The problems Game theory can solve and the promises it provides can add great value to humanity.

In order to understand the depths of the contributions of the Game Theory, we must understand the idea of Finite and Infinite Game.  

The finite game has known players, fixed rules, has an end point where there is one winner and there in one loser- a zero sum game. Like the game of chess, the game has two players, all the rules are fixed and cannot be changed by some external influence, either one of the kings gets the checkmate or the match becomes draw- no win or no lose- the game ends.

The infinite game is an eternal game- it goes on. The resources are infinite, the rules keep on changing, the players come and go. The infinite game is similar to what our life is. If one knows how to win an infinite game, then he/she can also win a life.

Simon Sinek has a beautiful book called “The Infinite Game” where he has explained how to win at an infinite game and thereby possibly at life. The insight from the idea of an infinite game is that the main goal of the game is to keep it playing. As the resources are infinite, players are infinite, rules are changeable- there is no endpoint for such game which will justify the worth of the winner. There is no winner.         

Most of the games in economics, finance may seem finite games for once but deep down, when explored further are the infinite games, our life is the best example of it. Simon Sinek has given many lectures, talks about the mindset for infinite game which are beautiful. They are beautiful because they reflect the philosophical nature of Game theory and its synergy to human decision making which is not rational all the times. Simon Sinek highlights on five headers while discussing the infinite games.

  1. Just cause- A Specific vision for the future which is yet to exist. It is powerful enough to motivate people, make sacrifice for it.
  2. Trusting teams- Creating room for improvements, improvements will lead to evolution, development. This will truly lift the human spirit. It is about the creation of psychologically safe environment where people can demonstrate who they are and improve over it to last longer in the game.
  3. Worthy rival- As the game is infinite- won’t end, the rival should always inspire one to elevate the game thereby strengthening both the sides. If the rival is not strong- worthy the game will end to some part but still new player will enter and perpetuate the game, thus the sustenance demands worthy rival.
  4. Existential Flexibility- Disruption for more effective development leading to evolution
  5. Courage to lead- Given the uncertainty of the outcome, a risk-taking attitude for the unknown but good future dependent upon the just cause is important to live through the infinite game.

Such ideas given for the infinite game can help build better organizations, better teams, better institutions.

“An infinite mindset embraces abundance whereas a finite mindset operates with a scarcity mentality. In the Infinite Game we accept that “being the best” is a fool’s errand and that multiple players can do well at the same time.”

– Simon Sinek, The Infinite Game

The Game theory itself represents an institution which has proved to become useful in not only economics but also in philosophy of humanity.

(We can deduce the optimal strategy for the engaging phone call game using Game theory. The optimal strategy is to do what both sides were doing before initiating the call. Thus, the one who tried calling first should continue calling whereas the one receiving the call should wait for the call rather than calling back! Please assume the rationality of your friend, willingness of your friend to accept the call, strong signal strength for the game!)

References and Further Readings:

  1. The Infinite Game by Simon Sinek
  2. Ross, Don, “Game Theory”, The Stanford Encyclopedia of Philosophy (Fall 2021 Edition), Edward N. Zalta (ed.)
  3. Game Theory: Definition, Role in Economics, and Examples by investpedia.com
  4. What game theory teaches us about war | Simon Sinek – TED Archive
  5. The Infinite Game for New York Times
  6. Strategic Dominance: A Guide to Dominant and Dominated Strategies by effectivology.com
  7. Photo of Jon von Neumann from Wikimedia and www.lanl.gov
  8. Photo of John Nash from Wikimedia and Peter Badge
  9. Photo of Simon Sinek from Wikimedia
  10. Memes from