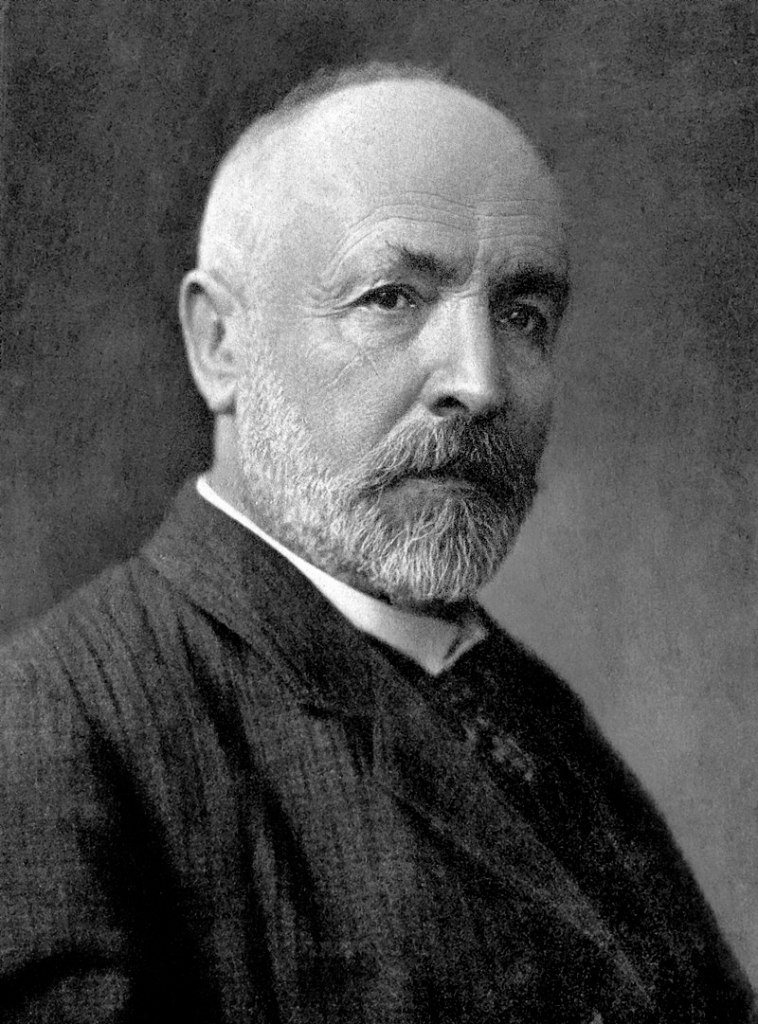Mathematics – Parts Per Billion

Sophie Germain- The Lady of Mathematics

Internet has literally exploded the branches of knowledge and made it accessible to any class, caste, creed, race, gender. We already owe to such technological revolutions for making knowledge truly accessible to everyone who desires to gain it. We all know the accessibility of knowledge was not open to such extents before. History has examples where certain class/group of people were restricted from not studying certain or all fields of knowledge. Starting from the early times in the popular history of knowledge, women were not supposed to study, take interests in the philosophical, technological ventures. You will find very few examples of female philosophers, scientists from the pages of history. Only in the recent century the liberalization of knowledge, awareness and realization of people thereby the social policies and advancements in technology have made knowledge accessible to all, especially women.

Today, I will be discussing about one such woman who is still not famous in mainstream and defied all the odds in her times to not only acquire but to contribute in our understanding of nature especially in the field of Mathematics.

This is about one of the greatest female mathematicians, physicists in the history of mankind called Sophie Germain. (Pronounced as jer-maw as in French)

The thing with mathematics is about the undefeated beasts it still holds. Given that most of us are already dreaded about the uncertainty of understanding/ failure/ lack of interest mathematics brings with it, any one unsolved problem till date in mathematics is enough to give an existential crisis to some of the greatest minds. Some of them are listed in Millennium problems and please note that the number of unsolved problems in mathematics in not finite and can haunt you forever. (Hence, Ignorance is bliss.)

One such problem haunted generations and generations of mathematicians and was supposed to haunt forever. It was the proof to the Fermat’s Last Theorem. The problem remained unsolved for centuries and whole efforts of mathematics were spent to prove it. Many greatest mathematicians, sharpest minds thought that it was unsolvable and left it as an unfruitful and wasted venture.

Finally, the problem was solved in 1995 by British mathematician Andrew Wiles. How he did that will be story for another time.

The important thing for this discussion is about the woman who took the first intellectual leap to crack “the easiest to understand but the most difficult to crack problem” in the history of humanity and mathematics. The times when she did this, mathematics was not the field for women. Women were not expected to study mathematics. I those times, woman were only expected to be “informed” (not study) about mathematics – rather scratch the surface of mathematics only to have an interesting conversation with men in parties, functions, meets.

The problem

Fermat’s Last Theorem states that for equation,

There exists no whole number solution for n>2.

The easiest and famous equation sitting in the neighborhood of this equation is the Pythagoras’s Equation for the hypotenuse of right-angled triangle, where x, y are the sides of right angle and z Is the hypotenuse of the triangle.

The problem is that this equation cannot be solved to whole number values of x, y and z if the value of n is larger than 2. The challenge is to prove that this is true. One can keep on substituting many values of x, y and z in order to check the output of values. If they are not getting the whole number solution then they can prove that the idea is true.

But mathematics does not work in that way. Even if you have computers to crunch the numbers, they cannot do it for eternity to infinity of numbers. Mathematics demands the rigor and logical proofs (not the experimental ones as in science) to prove any idea. If it is not proven logically and if there is no anomaly found for the idea then it is categorized as a conjecture.

In the old times, mathematicians actually hand-calculated the numbers to check whether Fermat’s last theorem holds true or not but could not find the real proof for the problem. The attempts done were for single values of n as in substituting values of n as 3, 4, 5 and so on.

The tricky part was that, it is itself difficult to prove the Fermat’s Last theorem for single value of n.

For n=3, one would still have to consider the infinite combinations of x, y, z to prove by mere number crunching. Even if every single human being solves the problem for each value of ‘n’ individually (which is impossible in itself), still it cannot be proven for all cases.

So, what every mathematician was doing was trying to prove the problem for specific case of certain value of ‘n’ in this equation. Meaning that everyone was solving the problem for the special case and it was difficult the generalize the solution, the proof.

The leap of generalization in Fermat’s Last Theorem

It was Sophie Germain, a woman mathematician amongst all men mathematician who made first successful attempt to generalize the proof of Fermat’s Last Theorem. The idea is based on certain prime numbers which are grouped as Germain Primes.

The strategy to prove Fermat’s Last Theorem was to prove the theorem for all prime number values of ‘n’. Prime numbers are building blocks of the all numbers in number theory. The are like smallest indivisible parts in numbers which cannot be divided into smaller numbers except themselves and one. It is already established and proved in mathematics that there are infinite numbers of prime numbers. It is very impractical to solve the Fermat’s Last theorem even from prime numbers one by one as they too are infinite.

What Sophie Germain did is to find a trend in the prime numbers and prove the theorem for such prime numbers. It is said that she got this idea from her factorization formula which is now known as “Sophie Germain factorization Identity”.

Here, you can notice that the last two steps tell us that this represents the number as its factors. If this single number (sum of 4th powers of two numbers) already has two whole number factors, then it cannot be prime as per the definition of prime numbers. The same idea can be used to check whether certain sums of numbers are prime numbers are not.

The insight from this identity is that, it can be used to check the 4^th power of equation in Fermat’s Last theorem if some adjustments are made. This same idea is reflected in the Sophie Germain’s attempt to prove the Fermat’s Last Theorem for a set of prime numbers.

Sophie Germain attempted the proof for some prime numbers today known as Sophie Germain primes.

A number ‘p’ is called as Germain prime if n=2p+1 also gives a prime number.

For, prime number p=2, new number n=2(2)+1=5 which is prime hence p=2 is Sophie Germain Prime.

For prime number p=3, n=2(3)+1=7 which is again prime hence p=3 is Sophie Germain Prime

But,

For prime number p=7 gives n=2(7)+1=15 which is not prime number hence 7 is not a Sophie Germain Prime.

So, if we adjust the Fermat’s Last Theorem equation to Germain Primes, we can develop some interesting insights.

Using the understandings from the Sophie Germain Identity and comparing them with the result above we can understand that as in Sophie Germain identity 4 as a coefficient and power of b, some solution exists.

Meaning that in order to have a solvable whole number solution to Fermat’s Last Theorem, either x, y or z needs to be multiple of the power to which they are raised i.e., ‘n’. And as this identity proves the composite (non-prime) nature of numbers from its outcome in most cases, there is possibility that the solutions will not be whole numbers and hence Fermat’ last Theorem Equation cannot have whole number solutions for n>2.

The most important aspect of this approach was that the idea does not discuss Fermat’s Last Theorem for certain value of n. It generalizes the equation for many numbers which was never done by any mathematician before.

Even more important than that was such progressive breakthrough in mathematics was established by a woman who was not expected to even study it. The times when Sophie established this breakthrough in mathematics, we must understand that women were discouraged from studying mathematics and it was assumed that math was “beyond their mental capacity”.

The Life of Sophie Germain

Marie-Sophie Germain was born in France in 1776 (almost 140 years after establishment of Fermat’s Last Theorem) in a house of a wealthy silk merchant. When she was 13, the French Revolution took the course of things and due to such sensitive environment, she was restricted to stay inside the house. The books in her father’s library became her friends where she was intrigued by the story of the death of Archimedes. (Archimedes was killed by a roman soldier only because he was so engrossed in his thoughts on a geometric figure that he could not answer the soldier’s question).

“How can a subject create such interest in a person that he couldn’t even think about his death!” was the curiosity which brought Sophie closer to mathematics. Though her times and parents would not allow her to study mathematics, she continued her journey alone to explore and learn mathematics. (Her parents tried removing warm clothing and candles from her room so that she will give up on studying mathematics but she continued her studies further).

As mathematics was not destined for women in her times, Sophie enrolled herself in the name of a man called as Monsieur Antoine-Auguste Le Blanc in École Polytechnique. She need not to attend the courses in person as the education was also available in the form of lecture notes. She audited the courses from the lecture notes hiding behind the name of a man Monsieur Le Blanc and completed her education.

Her intellect impressed one of the famous mathematicians and the instructor in École Polytechnique- Joseph-Louis Lagrange. The answer sheets, problem solving skills piqued interest of Lagrange to meet Monsieur Le Blanc in person where he found out that the problem solver is not a man but a woman called Sophie Germain. Good thing for mathematics, Lagrange became her mentor.

Carl Friedrich Gauss, the (as in “THE”) greatest mathematician of all times had also tried cracking the Fermat’ s Last theorem but left the pursuit as a hopeless one. Sophie Germain tried to explain her approach to solve the Fermat’s Last Theorem to Gauss through her letters as Monsieur Le Blanc. The approach of Sophie Germain again activated Gauss’s interest in Fermat’s Theorem and also he too was shocked upon her reveal as a woman.

“when a woman, because of her sex, our customs and prejudices, encounters infinitely more obstacles than men in familiarizing herself with [number theory’s] knotty problems, yet overcomes these fetters and penetrates that which is most hidden, she doubtless has the noblest courage, extraordinary talent, and superior genius.”
Carl Friedrich Gauss on Sophie Germain

Gauss and Sophie never met in person. Gauss actually made attempts at universities to grant her an honorary degree.

Sophie Germain and The Eiffel Tower

After Fermat’s Last theorem, Sophie tried herself in the development of theory of elasticity in a contest by Paris Academy of Sciences to develop a mathematical theory of vibration and elasticity. She was contested by the Simeon Poisson (known for Poisson’s Ratio). Later on, published works of Poisson’s on elasticity contained some works of Sophie Germain where she was not acknowledged.

In her third attempt to win the contest, after eliminating the errors and consulting with Poisson she published her theory and won the prize. She still was not able to attend the sessions of academy as the only women allowed were the wives of the members of the academy. After seven long years of membership, already having proven herself, Sophie attended the academy sessions because her friend and then secretary of the academy Joseph Fourier made the tickets available to her.

She had tried to republish her studies in elasticity separately after correction of errors to prove her worth against the works of Poisson. The academy still considered her work as trivial and they didn’t want her to entertain her further and rejected it. After the recommendation of famous mathematician and engineer Augustin-Louis Cauchy (known for Cauchy’s Integral Theorem), she published her work.

The same work on elasticity contributed to the development of an engineering marvel “Eiffel Tower” in Paris. She was not acknowledged even here.

The contribution of Sophie Germain to number theory was only revealed only because of a mathematician Adrien-Marie Legendre where he acknowledged her approach to prove Fermat’s Last Theorem.

Sophie Germain died of breast cancer aged 55 (June, 1831). She was the first woman who was not wife of a member to attend the French Academy of Sciences. She received her honorary degree posthumously from University of Göttingen in 1837 (6 years after her death)

The French Academy of Sciences started Sophie Germain Prize in 2003 in her name to honor her contribution to French Mathematicians.

Understanding the true nature of Mathematics- Gödel’s Incompleteness Theorem

Either mathematics is too big for the human mind or the human mind is more than a machine -Kurt Gödel

I remember the times in the school when we were introduced to the proofs of geometric theorems. There was this systematic template that you had to follow to secure full marks for the question. You would write the “Statement of the theorem”. Establish a geometry, define its components called “Drawing”. Then you would write “To prove”. Finally, you would follow the steps, based on the foundations you had in order to develop the final proof- “to prove”. The moment of relief was to rewrite the “to prove” statement again followed by “hence proved”.

Fun part of proving mathematical theorems was that, if one’s proofs were wrong or contained half written answers- he/she would fight for the marks of steps. I remember my friend (that one who used to study for wrong subject on wrong day) who wrote only the statement of theorem followed by “hence proved” or “LHS=RHS” in a (stupid) hope that it will yield at least one mark. Because of these theorems, there were two types of Mathematics teachers- The God mathematics teacher and the Devil mathematics teacher. No need to explain that the God mathematics teacher gave marks for the correct steps irrespective of the final proof. In short, mathematical theorems made us realize that there are some good mathematics teachers too. (a rare species!)

This funny and real experience reveal the true nature of mathematics.

Nature of Mathematics

Mathematics is made up of some systematic and logical steps which will reveal the nature of reality around us. Mathematics is not subjective; it is strong and resourceful to stand for itself. In simple words. Out of all the schools of thoughts mankind has developed, Mathematics is the purest of all. Mathematics never favors a thought just because some king, any political person or any spiritual leader has issued an order to call it true. Any mathematically proven true statement will remain true irrespective of the paths followed to reach it. Hence the reason, mathematics is the reflection of the truth rather the truth itself.

Mathematics has its own system of truths called “Axioms” and “logic” to decide whether any proposition is true or false. For any “given statement” to be true, there is a systematic approach of questioning the impact of “given statement” on other mathematical system which are already proven to be true. If the already “proven true mathematical systems” still follow their true behavior after involving the “given statement” – the statement is called as true. This is also what can be roughly called as “Consistency”. If given statement is true then it cannot be contradicted.

There is one idea for proving mathematical proofs involving “proof by contradiction”. You assume the proof to be false, then follow the logic and reveal that the outcome does not concur with the what was to be proved hence the assumption that it was false was false; hence whatever was to be proved true is true. Simple example can be given as follows:

Algorithm to decide whether 1+1=2 is True or False

One can simply ask some questions to conclude that 1+1=2 is a true statement. In whatever way one will negate the statement, the person will not reach to consistent and fixed result thereby proving the negation false.

From here on, our actual story starts,

The paradox of self reference in Set theory

Set theory is one of the most important (simple and complex simultaneously) in mathematics developed by George Cantor. A set can be collection of anything which follows certain rules. Set of cars will include all the cars you can see, set of planets in the solar system will include all the planets (excluding Pluto!).

What about a set of all sets- The set that contains everything?

Now the question comes, does the set that contains all sets, contain itself?

Does “the set that contains all the sets” contain itself?

If “the set that contains all the sets” does not contain itself then it leaves itself outside of itself- hence it doesn’t become “the set that contains all sets”- but it is “the set that contains all the sets”. This leads to contradiction, famously called as “Self-contradiction”. This was found out by Bertrand Russel.

Here is one more example:

Unlike our previous algorithm to prove 1+1=2, here the algorithm doesn’t break out to either true or false. It contradicts itself to be true or false hence gets in continuous loop. This is where, the mathematicians realized the true boundaries of what we can know and what we cannot know.

The Barber’s Paradox is also one funny example paradox of self-reference.

The two cases of self-contradictions explained above are verbal paradoxes, means that their outcome may be subjective based on what every person understands from the meaning of the words; they can be twisted to any person’s meaning or understanding. Mathematical truths are not like that, they are specific and cannot be twisted to make any desirable or subjective outcome.

The Ignorabimus

Boasting on the strong foundations and objective nature of Mathematics, many mathematicians called mathematics to be consistent thus they began the quest to prove the consistency of the mathematics. One of them was David Hilbert- one of the most influential mathematicians of all times. According to Hilbert, mathematics was consistent meaning for every mathematical true statement there exists no contradiction. It always follows only one single truth and its falsification of this truth does not exist. He had given a famous lecture to deny an idea called “Ignorabimus” (a latin maxim meaning “we will not know”- a topic for new and later discussion) saying that “We can know everything that is there to know and we will know that all”.

In reality, that was not the case. A day before this lecture actually happened- a logician called Kurt Gödel had proved that mathematics is not consistent. Means, contradictions can happen in mathematics. This was a shock for all the mathematics community. It’s like the truths in mathematics can be twisted to prove any wrong thing right.

Gödel had devised a method (purely mathematical) to prove that mathematics was not consistent.

It somewhat aligns with the thought process of Self-referential paradox or the paradox of set theory.

Gödel developed a system, this system is well explained elsewhere (find the link in Further readings section):

Gödel defined a number to each logical operator and number like for “and”, “or”, “not”, “successor” (means any number before the number), “addition”, “subtraction” and so on. Based on the statement, take for 1+1=2 he pulled out a mathematical function to give out a number which represents that statement. Similarly for all the axioms, Gödel pulled out these individual numbers. So, when you want to prove that 2+1=3, you will pull a number for that statement. The number pulled out from the expression 2+1=3 will have provable connection with the statement 1+1=2 thereby proving the statement 2+1=3 to be true.

Gödel developed the numbers for the axioms and proved that any statements can be proved from the operations on the numerical representatives of the statement to be proved.

For example:

When we enter 1+1=2 in a computer, the computer assigns the number and operator a unique code in 1s and 0s also known as ASCII (American Standard Code for Information Interchange) uses somewhat same idea to solve the addition operations to give output in a number containing 1s and 0s then converting it to the output display of calculator.

The fun starts when Gödel purely mathematically formulated number for a statement which was Self-referential paradox. The statement was like this:

“There is no proof for the statement with Gödel number g”

Meaning, that there exists no proof for the statement which number g indicates in the system out of which it has been created. The statement is unprovable

The Paradox-

There are two cases to be evaluated:

If the above Gödel statement is false means, there is a proof. But according to Gödel statement there is no proof in the system Gödel created, thereby creating a contradiction.
If the above Gödel statement is true means it is not provable from the Gödel system.

Either of the cases evaluated above lead us to conclude that the current system in which the statement was created will not have the proof for some true statements thus making it incomplete.

You will need to jump out of the system to create a new proof to evaluate the truth of the system because given system has insufficient axioms to prove the new statement to be true, hence the new statement itself becomes a new axiom.

The combination of this axiom with the already existing axioms creates a new system.

For example:

Two parallel lines will never intersect each other

This is true when you are in Euclidean Geometry where right angles and plane of paper are of prime importance. Where the plan of paper has no curvature

But when you are able change the curvature of the paper where parallel lines are drawn, you can make them intersect.

The no intersection idea of parallel lines is the basis of Euclidean geometry but their intersection is not provable in the Euclidean geometry itself. You have to create non-Euclidean geometry (Hyperbolic, Elliptical geometry discovered by Lobachevsky and Gauss) in order to prove the point.

This means that the statement that Parallel lines may intersect has to be assumed as true with no proof in Euclidean geometry, once accepted as the truth it developed a new a system called non-Euclidean geometry where the system became more complicated.

This brings us to one final question that- Can we know everything that is there to know in mathematics given that it is the purest form of truth?

And the answer is No.

The Gödel’s incompleteness theorem proves that there always will be some true statements in a system where there will be no proof to prove them true. The acceptance of these statements as true will lead to development of new system.

The challenge for mathematicians is that accepting something to be true without having a proof to call it the truth. If some mathematical statement when tested to be true to every mathematical simulation proves to be true, should we accept it as the unprovable truth?

This highlights the incompleteness of Mathematics.

The Millennium problems and Gödel’s Incompleteness theorem

There are some problems in mathematics famously called as the millennium problems. The problems yet not proved and if proved true will completely revolutionize the mathematics thereby creating a new system of the axioms and their combinations.

The Goldbach conjecture, Riemann Hypothesis, Nature of the roots of the Navier-Stokes Equations are some of them.

The great thing about the Gödel’s Incompleteness theorem is that the idea of numbering the statements led to the development of machine language, programming and developments of early computers.

There is a concept in artificial neural networks called grey box model where you try to predict the outcome of events based on the already fed relations between variables, interactions between them and their outcomes. We actually do not know what is happening inside the grey box models of the neural networks but we know that when fed with enough data the outcomes are true based on real conditions.

The Gödel’s incompleteness also makes us question our biases. If something true is not provable, how would you prove it to be true OR if it’s not provably true is it really true? ( One of the millennium problem possible unprovable known as Fermat’s last theorem is proved after whopping 350 years) This also highlights how difficult it is to develop a purely original mathematical idea, how small amount of time we have as a human to discover the marvels of the nature, universe around us.

The conclusion is that there always will be something that is not complete. There always will be something that we may not know. There always will be something that needs development of new foundations to be true. There always will be something in this universe (and may be multiverse) that still needs to be discovered which will give us new perspective to look at things.

Ignoramus et ignorabimus
we do not know and will not know