Kurt Gödel – Parts Per Billion

The Trilemma of the Truth and the Skepticism

Skepticism deals with the attitude of questioning our beliefs based on an idea that our perception of reality through our senses and personal experiences may totally different from “the actual reality”. The Münchhausen Trilemma and Agrippa’s Five Tropes from epistemology may guide us on how to suspend a judgement and how assign truth value to every belief in our lives.

Why the philosophical search for the ultimate universal truth is useless?

An Existential Meme Caption and Its Resolution

Since the invention of social media, some images (especially the certain classic meme templates) have stood the test of time. These images keep on circulating and there comes a moment when that image reinvents itself in new format, it brings some new argument with different type of humor. See the following image for example:

Funnily enough, this image always comes with a thoughtful (supposedly) caption as follows:

“Just because you are right, does not mean, I am wrong. You just haven’t seen life from my side”

Given that the argument presented in this caption demonstrates the subjectivity of the everyone’s perspective, it is really futile to discuss what to exactly extract or understand from this caption.

For example, if this was the scenario where knowing the true value would save a person’s life then knowing the truth becomes the necessity and all of us know that this wouldn’t have saved that precious life which was dependent the true answer. There is no definite answer for this argument because it invokes subjectivity in the argument. People use this image and the said caption to express their inability to prove the truth value of their argument, especially their emotions.

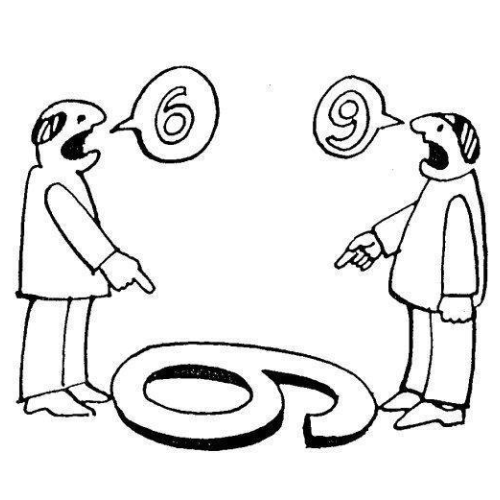
Now, in recent time this image resurfaced with a new argument which blew my mind the moment I saw it. The reinvented image looks like this:

“How a mathematician/ an engineer solved the conflict”

You must appreciate wit and sense of humor of the person who modified the argument presented in the original image.

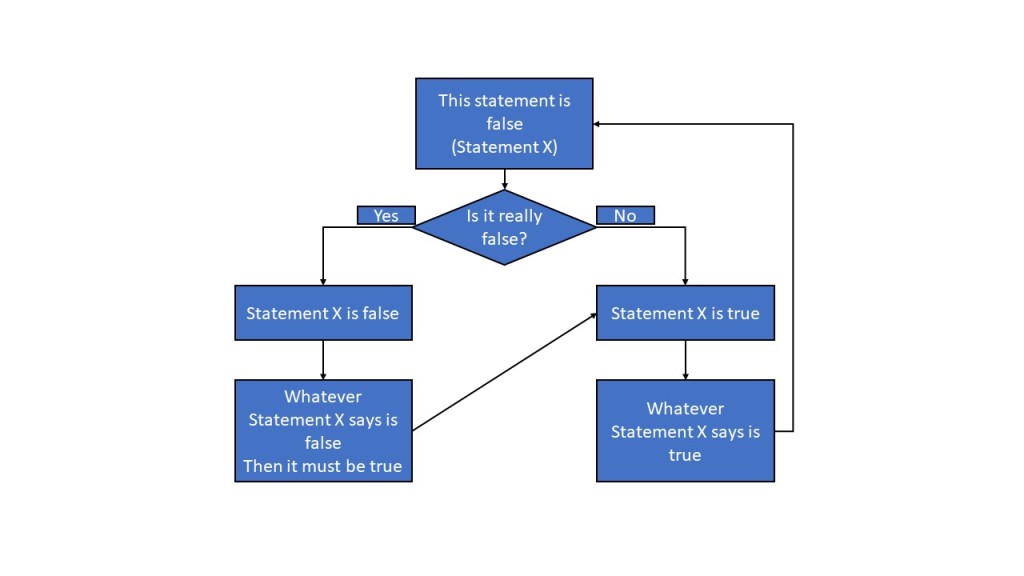
There Is No Final Truth.

This simple evolution of a very common internet template invites a question. What is the real truth? What is the truest truth? What is that one answer that can answer all the questions? If something exists in truth, then how would I verify that it is “the truth”?

At first one might think that these are such foolish questions. Truth can be established by experimentation, demonstration, repeatability/ reproducibility, comparison, consistency, contradiction/ counterexamples.

Take for example,

Q1: how would one calculate the time taken by the ball dropped from certain height on the Earth to reach the ground?

A1: The answer is by using Newton’s kinematic equations.

Q2: How the kinematic equations were developed?

A2: By using Newton’s law of gravitation and the law of motion

Q3: How these laws were developed?

A3: Newton studied the motion of moon and earth, developed some mathematics to explain that behavior. That math remains consistent to explain the scenario of the motion of the ball dropped from certain height.

Now from here the real fun begins,

Q4: If Newton’s law of gravitation and laws of motion are consistent and hence true then why did they fail to explain the different/anomalous motion of the planet Mercury around the Sun?

A4: The truth presented in Newton’s laws of gravitation and motions are a special case of the higher and more inclusive, exhaustive truth of Einstein’s relativity.

Q5: Why Newton’s truth is not the complete/ ultimate truth?

A5: Newton assumed Gravitational as a universal force of attraction, inertia of every object in the universe, concepts of the balanced force.

Q6: Did Newton made mistake in “assuming” certain things for the sake of establishing the proof and its mathematics? Because, Einstein certainly didn’t assume those things and still his theory of relativity can prove the arguments covered by Newton.

A6: Yes, looks like Newton assumed gravity as a force of attraction where things will get “pulled” towards heavier objects or fall into them. Whereas Einstein established this as wrong and proved that Gravity is actually a “push” created due the curvature in space-time.

Now from hereon, if one remains careful enough then that person can land into the territory of quantum mechanics to prove that Einstein was wrong (in a way). The failure that connect the Theory of relativity and quantum mechanics is why we are still uncertain what is the ultimate truth that will answer all the questions there exist. (Trust me the answer is definitely not “42”!)

So, if we keep on asking the question to each and every truth, will we reach the ultimate truth? Will that be the ultimate knowledge? Will that help us define the absoluteness of the knowledge?

Philosophers have argued (literally and figuratively) for centuries about the acceptability of any truth as “the truth”. Epistemology deals with the theory of knowledge, how a belief and opinion differ from the truth, if given argument is true then how it becomes the truth- what is its validity, justification?

So, when one starts to question things continuously there will be three possible cases explaining how the things will end into. This condition is famously known as Agrippa’s Trilemma or the Münchhausen trilemma in philosophy.

In really simple words, the trilemma says that it is impossible to prove whether certain truth is really true because at the last end of this truth there will always be some unjustified, non-contradictory fact which cannot be proved by using other proofs in existence.

Let see in detail what is this trilemma and the its legacy in epistemology.

The Münchhausen Trilemma

Baron Münchhausen is a fictional character created by German writer Rudolf Erich Raspe in his book “Baron Munchausen’s Narrative of his Marvelous Travels and Campaigns in Russia”. Münchhausen is a person who has done many impossible things like fighting a forty-foot crocodile, and traveling to the Moon. The book is a satire. (Baron Münchhausen is German Don Quixote per say!)

So, there is a story where Baron Münchhausen is drowning in the water while riding on his horse but soon he realizes that he can lift himself from the water just by pulling his hair. Hence, he pulls his hair and comes out of that mire/ quicksand with his horse.

Münchhausen saves himself along with the horse from drowning by pulling himself by his hair!

Do you understand how it worked? How could one pull himself out of an unsupported marshy land without any support? Where did Münchhausen pivot to rest himself? The story is foolish!

So, how did Münchhausen come out of mire without any support? If he was successful in his rescue, he would have definitely used some pivot, some support!

In the similar emotion, any argument to be proven true will need another supporting true argument. This “primary supporting true argument” will also need another “secondary supporting true argument”. You might have understood where we are going with this. If this keeps on progressing further and we keep questioning the complementary true arguments which are supporting the main truth then we will end up in three possible scenarios, which are “the trilemmas” as follows:

If we keep on questioning anything, the proofs will:

Given proof will be followed by other distinct proofs which further will be proved by other more distinct proofs leading to infinite chain of proofs – The regressive argument
A proof will be proved by another proof based on the prejudice that it is consistent in many cases so, as it is consistent then it must be true hence the main proof is true – The circular argument
The proof will be accepted as the truth as there is no proven counterargument or any contradicting observation to falsify it – The dogmatic argument

Resolving the Trilemma

Explaining these trilemmas, we can say that these three trilemmas can be solved by following ways:

Infinitism: there will be an infinite chain of justifications for every truth. It will never end.

Remember that child who annoys their parents with a new question to every answer they give. That child indirectly knows infinite reasoning! (somehow!) A “patient” parent can go on answering that child’s each and every question!

Coherentism: there will be recurring loop of beliefs based on some other beliefs. These beliefs will prove each other.

You know your friend is telling you the truth because you have always seen him/her telling you the truth. It is consistent with his behavior. As you “believe” that he/ she tells the truth, whatever is told by them would also be true. (But who knows!)

Foundationalism: the chain of justifications will end at an argument which is accepted as the truth without any other proof and/or because there is no contraction available to this argument. It becomes accepted as an axiom which lies at the foundation of everything.

The matter was accepted to be made up of smallest invisible particle called atom and based on that many good theories explaining reaction stoichiometry, formation of molecules and thereby compounds was explained. We now know that atom can constitute further divisible particles thereby upgrading the theory further on to cover more generalized cases till quantum systems.

Similarly, Newton’s ideas which we discussed in the start rested on some foundation which proved many truths based on that foundation. It was the failure of that foundation which could not explain the motion of mercury. Einstein’s new foundation embraced wider foundation where Newton’s math becomes a special case. We will keep on upgrading our foundations.

Skepticism, Agrippa and the Suspension of the Judgement

There was a school of Greek philosophers who questioned the very existence of the knowledge. They were “skeptical”, “doubtful” about everything thereby forming the school of Skepticism in philosophy. The reason to question everything available around us was due to the ways through which we understand these things. There is a gap between how we experience things around us through our senses and what these things really are. (What we see in desert looking like a lake is actually a mirage) There will always be some gap between appearance and reality. So, what we are believing to be true does not necessarily requires to remain true. The reality might be totally different. Not only different but reality can be subjective meaning that what a person has experienced from a thing can be totally different from what another person has experienced, and both stand true because of the individuality of their ways of experiencing the reality. Both sides will be true due to distinct and unprovable subjectivity. Bertrand Russel in his book the Problems of Philosophy has clearly discussed this as the limitations of our senses and the nature of reality. these limitations of our senses bring in that subjectivity in our truths hence they are our versions of truths which may be the truths for others. So, the early idea was to question everything to suspend both beliefs, experiences or the versions of the truth.

The problem which is created here is that if people become doubtful about everything around them, then they will end up in questioning their own existence. This question of existence will further lead to infinite chain thereby rendering useless, worthless, and futile venture. That is exactly why Socrates pursued ethics where “Why to live?” is not that much important and where “How to live?” is much more important.

One of the important philosophers called Pyrrho ((360-270 BCE) traveled with the army of Alexander to India where he met some “naked philosophers” (gymnosophists) who explained to him the reality of life. That there is no such thing as true or false, nothing is just or unjust, neither is honorable or dishonorable. No belief or experience is true or false. From these naked philosophers (I think these were the ancient groups of “Naga Sadhus” which exist even in our time today). These learnings focus on not having any judgement thereby rejecting any judgement, suspending any judgement.

This gave rise to the formation of five tropes for suspension of judgement which were developed by Agrippa who came later and expanded the understandings of Pyrrho.

These five tropes go like this:

When the views are conflicting between common people and the philosophers then we must suspend that judgement – unacceptable due to inconsistency – Dissent
When one is justifying a claim then that claim must be appealed by a prior claim which will end in infinite regress, so we must suspend that judgement – Progress ad infinitum
Everything is relative, things appear right or wrong based on the condition in which they were observed and the environments in which they were judged, so we must suspend that judgement – Relation
When a judgment is proved to be true based on an assumption and if that assumption itself is unsupported then we must suspend that judgement – Assumption
When a truth invokes another proof which creates the circularity of justifications then we must suspend that judgement – Circularity

The beauty of the Agrippa’s five tropes is that it brings in the relativity in our process of understanding the truths of our lives. I would say that Agrippa solved the problem of establishing the truth by the process of elimination. In a very smart way, instead of proving something directly to be true, we can work around the facts surrounding given argument. Eliminating the arguments in the proof by implementing these five tropes can at least reduce the size of the problem thereby keeping all the possibilities of proving it to be true always open. The beauty is in the opportunities to upgrade the foundations!

This philosophy of skepticism created the foundation of modern philosophy and thereby modern science and mathematics. Some ideas explained in this trilemma remain consistent with the Kurt Gödel’s Incompleteness Theorem which explains why mathematics rather the reality itself is inconsistent. There will always be something unprovable in given domain of system which will demand to expand that system to a totally new system of knowledge thereby upgrading the existing foundations of our understanding of the nature and the reality and thereby our fields knowledge. That is exactly why Newton’s ideas even though were limited to some special cases are important because Einstein wouldn’t have had the foundation to build upon something. We will always be creating some general understanding of the universe which later will surely become a special case in our understanding. That is also why questioning everything is important in the process of developing fundamental understanding. It is the philosophy of skepticism which empowers us to stay humble and rediscover the reality in which we already exist.

The Book of Five Rings – the Book of the Void

The final book from the Book of Five Rings by Miyamoto Musashi may seem like a last page reading with very few paragraphs but it gives deep insight into the knowledge that is yet to be gained by the person and the knowledge which lies beyond the limits of the humanity. The Book of the Void is the most concise treaty on the extent of our knowing, our ignorance and that knowledge which we would never know due to the mortal limitations. Miyamoto Musashi’s idea of the absolute wisdom through the concept Void transcends the boundaries of human life and time.

Miyamoto Musashi’s philosophy for 21^st century

After disseminating his lifelong wisdom in a very systematic way through four books named as the Ground Book, the Water Book, the Fire Book, and the Wind Book representing the philosophies to fight the battles, wars and survive through the challenges of the life, Miyamoto Musashi concludes his learnings in last book – the Book of the Void. On the scale of writing, it is not even a book. The readers will feel like they are reading the last page of the book. This shortness of the last book – the book of Void is very intentional by Miyamoto-san. Again, as his suggestions go – one has to really appreciate what he is trying to communicate – the wisdom that which cannot be expressed, conveyed through words.

The main purpose of the Book of the Void is to make the readers aware of the things and the wisdom that they can never know. There is one danger in this process especially for those who learn only by themselves (-without a real teacher always in front of them) which Miyamoto-san was very well aware of. He tries to complete this cyclical process of gaining wisdom through self-learning in this Book of the Void.

“What is called the spirit of the void is where there is nothing. It is not included in man’s knowledge.”

First, he clarifies what this is all about. Miyamoto-san first brings out the elephant in the room that there will always be something that you could never know.

“By knowing things that exist, you can know that which does not exist. That is the Void.”

The Void thus represents the wisdom that lies beyond all that can be known by every human being. Now there is one catch in this idea. A normal person who has just started his journey on the path of wisdom will not know everything initially. So, whatever he/she does not know right now is new for him/her. Does this new wisdom which that person was unaware, which discovered during the journey represent the Void? The answer is – No. The Void is not the gap between your current understanding, current knowledge, and the knowledge you are yet to gain or understand. The Void is that which can never be known even when ‘everything that is there to know’ is known completely. And that itself is really humbling. It is about the limits of how we learn, understand the world around us. Miyamoto-san as the great teacher makes every reader aware of what the limitations of our understandings are. He wants everyone to understand that even when you know ‘everything that is there to know’, there still will be something left out because of the limitations of the ways we perceive the reality.

“People in this world look at things mistakenly, and think that what they do not understand must be the void. This is not the true void. It is bewilderment.”

Here, Miyamoto-san very smartly makes the reader aware of what they call the Void may be and mostly will be the knowledge they are yet to gain. Again, as I explained earlier, the Void is not the gap between what you know and what all there is to be known by you. For every learner, whatever they haven’t experienced before will be new knowledge to them (which literally is the definition of ‘new’!) That will create the illusion of Void for them but the path is way long for the pursuit of true wisdom. We have this tendency of treating every new experience we come across as a very special experience and there is nothing wrong in it, but also creates an illusion of knowing the special wisdom in the person. This instigates the illusion of knowing something extraordinary, of knowing everything in the mind of that person.

Miyamoto-san thus advises the readers to recognize the confusion between the common knowledge and the real Void – the knowledge lying beyond everything that can be known.

In very simple and short words, Miyamoto-san is trying to show the expanse of the true ‘wisdom of life’ to the readers so that they will be humbled by what very small amount they know and they can know throughout their limited lifetime. Miyamoto-san idea of Void is intended to remain on the path of learning throughout the life with the awareness that there will always be something beyond our current understandings of the nature.

Being aware of the infinite extents of that which can be never known, one creates the curiosity to know everything that is there to know; it also brings in the humility for what very little one knows.

The idea of Void by Miyamoto-san is about intellectual humility and the limitations of how we understand the world around us.

Let us keep the idea of the Void aside for now. The things that we can know, the wisdom that we can have themselves are so vast in their expanse that a single mortal life cannot be sufficient to learn and grasp each and everything that is there to know. This will easily overwhelm a new learner rather everyone on such journey. Miyamoto-san knew this hence he proceeds with the ways to clear this confusion and such overwhelming feelings.

“To attain the Way of Strategy as a warrior you must study fully other martial arts and not deviate even a little from the Way of the warrior. With you spirit settled, accumulate practice day by day, and hour by hour. Polish the twofold spirit heart and mind, and sharpen the twofold gaze perception and sight. When your spirit is not in the least clouded, when the clouds of bewilderment clear away, there is the true void.”

In simple words, the way to get everything big is to start small and build over it, follow the truest path step by step instead of getting overwhelmed by the length of the journey. Once the person becomes aware of the process, the things built over the time will help him/her to distinguish between the that which is known, that which is yet to be known and that which can never be known.

You will notice in every part of the Book of the Five Rings especially in the Wind book, Miyamoto-san suggests to learn the techniques of the other schools from a broader perspective. Even after being the greatest swordsman of his time, he was completely aware that there will always be something which can improve his existing techniques. There will always be some better ways to do the same thing. This newer, creative, and out of the box thinking is only possible for the person who understands the limitations of his mind, who is truly humble even after gaining all the wisdom in the world. Only the idea of the Void can show a complete scholar the extents of what he/she knows.

Miyamoto-san mentions the spirit of heart and mind which are emotional and intellectual aspects of personality. He further mentions the perception and sight which are the abilities to see beyond what is shown and to see the bigger picture. The journey for the true wisdom is about development of our emotions, intellect, perception, and vision. That is what life actually is! What a thought by Miyamoto-san!

“Until you realize the true Way, whether in Buddhism or in common sense, you may think that things are correct and in order. However, if we look at the things objectively, from the viewpoint of the laws of the world, we see various doctrines departing from the true Way. Know well this spirit, and with forthrightness as the foundation and the true spirit as the Way. Enact strategy broadly, correctly, and openly.”

Miyamoto Musashi holds the last but the most important (and the secret trick) in the journey for the wisdom of the life. Actually, he already hinted this secret in the early part of the Book of the Five Rings. Miyamoto-san explains that when the person on the journey for the wisdom will reach the ultimate spot (and not the end of the journey- the journey has no end – it continues in the Void) then he/she will realize that the vast expanse of knowledge that they were getting overwhelmed in the early part of their journey are actually created from the main true path of the absolute wisdom. The vast expanse of the knowledge was created due to many deviations from the ultimate path. The absolute wisdom will have that clarity as Miyamoto-san explains. That is the exact reason why he already said

“If you know the way broadly, you will see it in everything”

Once you get the absolute clarity of what you know then you will never feel the need to know each and everything. You are zero and infinity at the same time, you are nothing and everything at the same time. You will try to understand everything based on the absolute wisdom you already have as all the remaining knowledge is just a deviation from that absolute wisdom.

“In the void is virtue and no evil.”

The acceptance of that which can be never known will actually make the person humble. Many will think that the idea of not knowing everything will actually create maniacs due to that unsettling urge to know everything but the exactly opposite will happen. When one accepts that the journey for the wisdom is a never-ending, then the smartest choice is to embark on this journey with minimum possible baggage. The true scholar will get rid off every deviated knowledge from the path of the true wisdom to reduce their load in this journey, they will use their limited but ultimate wisdom in every possible and new way to understand the new knowledge and the knowledge which cannot be known.

You must appreciate how great thought Miyamoto-san put forward many years ago with close to zero resources. That is what is great about the Book of the Five Rings and especially the Book of the Void.

The Book of Void actually speaks about everything through the idea of nothing. This can be put down into some words only by the scholars like Miyamoto Musashi. That also the reason why the Book of Five Rings is not just a guide for war strategy and the ways of the warriors. The Book of Five Rings is more than that, it is about the ways to live a life full of true wisdom. True wisdom holds everything in the idea of the awareness of nothing.

The Spirit of the Void for the modern world

“Real knowledge is to know the extent of one’s ignorance”
Confucius

The initial realizations of the idea of the Void are presented to make the readers aware of what small they actually know and what vast they are yet to know. When one accepts that there is still more to know and learn many things and even after knowing/learning everything, there will be something which can never be known due to the limitations of human life, at that exact moment the person becomes the container to the ultimate wisdom.

Void and the Incompleteness of the Mathematics

Modern mathematics and the development of completely new mathematical concepts are based on the world-famous Gödel’s incompleteness theorem. In simple worlds, certain truths in a system must be accepted true without a proof (and there are no contradictions to them till now) to prove all the remaining truths of the system. If in such system a new fact arises which cannot be proven by any existing truths and is never contradicted then such non-contradicted and unprovable truth will create bigger system of newer truths. (you can read in detail about this in my older post). The new uncontradicted, unprovable truth in the system lies out side the existing system of truths. It can be only understood by the person who is open to new possibilities outside the existing system.

The Void and The Dunning-Kruger Effect

Miyamoto-san even in his days was aware of this world-famous psychological effect now that we have a proper name for it. Miyamoto Musashi knew how half-knowledge – limited knowledge creates the illusion of knowing everything and can even blind the master of masters personality. He wanted the new learners to remain humble not get overconfident during the start of the long journey and he knew that the one who has traveled enough through this journey will have the humility for what great they have achieved. (see my older post to know more about the Dunning Kruger effect)

“The opposite of knowledge is not ignorance, it is the illusion of knowledge”
Stephen Hawking

The Void and Ralph Waldo Emerson’s Modern Scholar

Miyamoto-san’s idea of the Void also highlights how we are only able to learn what we are able to grasp. This actually creates a biased learning process, which is dominant in those who learn things on their own. Even for people who are masters of their fields and have proper guidance available externally, it is impossible to learn something new and groundbreaking unless they are receptive towards it. Ralph Waldo Emerson in his world-famous speech The American Scholar explained how exactly this learning works. (read in detail about the American scholar in my older post1, post 2, post 3)

The Void and Einstein

Einstein’s idea of relativity was rejected by many scholar scientists in the early stages because they were unable to accept and understand the ideas of higher dimensions in the fabric of the space-time. (That is exactly why Einstein is known as a peerless genius!) So, you can only learn what you are able to perceive and grasp. Miyamoto-san’s philosophy of Void encourages to become open to that which cannot be known which lies beyond our grasp.

The Void and The Quantum Mechanics

While we are on the cusp on the quantum mechanical revolution in modern world, it was Max Planck in quantum mechanics’ early emergence when he quoted about the nature of the reality we live in and our inability to understand such quantum mechanical reality. Upon understanding the mind-boggling nature of the quantum mechanics Max Planck maybe got a peek into the Void – that which can never be known due to our physical limitations. For a swordsman as Miyamoto Musashi, the philosophy of the Void stood the test of the time.

It also shows how absolute wisdom remains consistent throughout the times, branches of knowledge and generations. (find more about how we have realized the existence of Void through one interesting concept in QM in my older post)

Conclusion

Thus, the Book of Void by Miyamoto Musashi is about remaining humble about the extents of the knowledge we have right now, the knowledge that is yet to be known and the knowledge that is beyond the limits of our understanding which is the real Void.

The concept of Void clarifies three main points:

– 1 –

What you know is very small compared to what all there is which can be known.

– 2 –

You can know everything that is there to know and when you will know everything that can be known you will understand that everything that can be known is just the result of the many deviations from the absolute knowledge.

Knowing everything is not about understanding everything individually like a memory bank, rather it is knowing a thing in its entirety and every perspective

This clears one fundamental doubt which everyone has in their own learning journey. We think that if we know many things then we will have knowledge of everything. For the same reason we think that a wise man has many tools in his bag to deal with every problem.

But it is exactly opposite when it comes to the concept of wisdom through Void.

A wise man knows single concept which touches all that is there to know, this single concept brings in the clarity. A true wise man never carries a bag full of different tools to solve different problems, he carries the distilled understanding of how to develop the tools according to the problem.

Thus, once you are able to know everything that is there to know you will find a single thread connecting to all such fields of knowledge. You will never get overwhelmed by the amount of information and expanse of the various fields of the knowledge. That single thread of your wisdom will bring clarity, will bring in virtue in your life, will calm down your mind

– 3 –

When you will succeed in knowing everything then you will truly understand the boundaries of how you understand the universe. This will be the moment when you will accept the existence of the true Void. This acceptance will make you humble and even after knowing everything that is there to know you will embark on the new journey of that which can never be known. That will be your transcendence.

One has to very deeply think and understand and appreciate how Miyamoto Musashi in his very short but important “Book of the Void” distilled the fundamental wisdom of humanity. No wonder this concept of Void is always peeking its head out in different events, different lives, different breakthroughs, and different eras of the humanity. The truest wisdom always remains consistent throughout and it never fears to upgrade itself based on the new learnings. The Book of Void is about what small amount we actually know, what vast ocean that is there to know and what massive expanse lies beyond that ocean as the Void – the world beyond our understandings.

Links for further reading:

Understanding the true nature of Mathematics- Gödel’s Incompleteness Theorem

Either mathematics is too big for the human mind or the human mind is more than a machine -Kurt Gödel

I remember the times in the school when we were introduced to the proofs of geometric theorems. There was this systematic template that you had to follow to secure full marks for the question. You would write the “Statement of the theorem”. Establish a geometry, define its components called “Drawing”. Then you would write “To prove”. Finally, you would follow the steps, based on the foundations you had in order to develop the final proof- “to prove”. The moment of relief was to rewrite the “to prove” statement again followed by “hence proved”.

Fun part of proving mathematical theorems was that, if one’s proofs were wrong or contained half written answers- he/she would fight for the marks of steps. I remember my friend (that one who used to study for wrong subject on wrong day) who wrote only the statement of theorem followed by “hence proved” or “LHS=RHS” in a (stupid) hope that it will yield at least one mark. Because of these theorems, there were two types of Mathematics teachers- The God mathematics teacher and the Devil mathematics teacher. No need to explain that the God mathematics teacher gave marks for the correct steps irrespective of the final proof. In short, mathematical theorems made us realize that there are some good mathematics teachers too. (a rare species!)

This funny and real experience reveal the true nature of mathematics.

Nature of Mathematics

Mathematics is made up of some systematic and logical steps which will reveal the nature of reality around us. Mathematics is not subjective; it is strong and resourceful to stand for itself. In simple words. Out of all the schools of thoughts mankind has developed, Mathematics is the purest of all. Mathematics never favors a thought just because some king, any political person or any spiritual leader has issued an order to call it true. Any mathematically proven true statement will remain true irrespective of the paths followed to reach it. Hence the reason, mathematics is the reflection of the truth rather the truth itself.

Mathematics has its own system of truths called “Axioms” and “logic” to decide whether any proposition is true or false. For any “given statement” to be true, there is a systematic approach of questioning the impact of “given statement” on other mathematical system which are already proven to be true. If the already “proven true mathematical systems” still follow their true behavior after involving the “given statement” – the statement is called as true. This is also what can be roughly called as “Consistency”. If given statement is true then it cannot be contradicted.

There is one idea for proving mathematical proofs involving “proof by contradiction”. You assume the proof to be false, then follow the logic and reveal that the outcome does not concur with the what was to be proved hence the assumption that it was false was false; hence whatever was to be proved true is true. Simple example can be given as follows:

Algorithm to decide whether 1+1=2 is True or False

One can simply ask some questions to conclude that 1+1=2 is a true statement. In whatever way one will negate the statement, the person will not reach to consistent and fixed result thereby proving the negation false.

From here on, our actual story starts,

The paradox of self reference in Set theory

Set theory is one of the most important (simple and complex simultaneously) in mathematics developed by George Cantor. A set can be collection of anything which follows certain rules. Set of cars will include all the cars you can see, set of planets in the solar system will include all the planets (excluding Pluto!).

What about a set of all sets- The set that contains everything?

Now the question comes, does the set that contains all sets, contain itself?

Does “the set that contains all the sets” contain itself?

If “the set that contains all the sets” does not contain itself then it leaves itself outside of itself- hence it doesn’t become “the set that contains all sets”- but it is “the set that contains all the sets”. This leads to contradiction, famously called as “Self-contradiction”. This was found out by Bertrand Russel.

Here is one more example:

Unlike our previous algorithm to prove 1+1=2, here the algorithm doesn’t break out to either true or false. It contradicts itself to be true or false hence gets in continuous loop. This is where, the mathematicians realized the true boundaries of what we can know and what we cannot know.

The Barber’s Paradox is also one funny example paradox of self-reference.

The two cases of self-contradictions explained above are verbal paradoxes, means that their outcome may be subjective based on what every person understands from the meaning of the words; they can be twisted to any person’s meaning or understanding. Mathematical truths are not like that, they are specific and cannot be twisted to make any desirable or subjective outcome.

The Ignorabimus

Boasting on the strong foundations and objective nature of Mathematics, many mathematicians called mathematics to be consistent thus they began the quest to prove the consistency of the mathematics. One of them was David Hilbert- one of the most influential mathematicians of all times. According to Hilbert, mathematics was consistent meaning for every mathematical true statement there exists no contradiction. It always follows only one single truth and its falsification of this truth does not exist. He had given a famous lecture to deny an idea called “Ignorabimus” (a latin maxim meaning “we will not know”- a topic for new and later discussion) saying that “We can know everything that is there to know and we will know that all”.

In reality, that was not the case. A day before this lecture actually happened- a logician called Kurt Gödel had proved that mathematics is not consistent. Means, contradictions can happen in mathematics. This was a shock for all the mathematics community. It’s like the truths in mathematics can be twisted to prove any wrong thing right.

Gödel had devised a method (purely mathematical) to prove that mathematics was not consistent.

It somewhat aligns with the thought process of Self-referential paradox or the paradox of set theory.

Gödel developed a system, this system is well explained elsewhere (find the link in Further readings section):

Gödel defined a number to each logical operator and number like for “and”, “or”, “not”, “successor” (means any number before the number), “addition”, “subtraction” and so on. Based on the statement, take for 1+1=2 he pulled out a mathematical function to give out a number which represents that statement. Similarly for all the axioms, Gödel pulled out these individual numbers. So, when you want to prove that 2+1=3, you will pull a number for that statement. The number pulled out from the expression 2+1=3 will have provable connection with the statement 1+1=2 thereby proving the statement 2+1=3 to be true.

Gödel developed the numbers for the axioms and proved that any statements can be proved from the operations on the numerical representatives of the statement to be proved.

For example:

When we enter 1+1=2 in a computer, the computer assigns the number and operator a unique code in 1s and 0s also known as ASCII (American Standard Code for Information Interchange) uses somewhat same idea to solve the addition operations to give output in a number containing 1s and 0s then converting it to the output display of calculator.

The fun starts when Gödel purely mathematically formulated number for a statement which was Self-referential paradox. The statement was like this:

“There is no proof for the statement with Gödel number g”

Meaning, that there exists no proof for the statement which number g indicates in the system out of which it has been created. The statement is unprovable

The Paradox-

There are two cases to be evaluated:

If the above Gödel statement is false means, there is a proof. But according to Gödel statement there is no proof in the system Gödel created, thereby creating a contradiction.
If the above Gödel statement is true means it is not provable from the Gödel system.

Either of the cases evaluated above lead us to conclude that the current system in which the statement was created will not have the proof for some true statements thus making it incomplete.

You will need to jump out of the system to create a new proof to evaluate the truth of the system because given system has insufficient axioms to prove the new statement to be true, hence the new statement itself becomes a new axiom.

The combination of this axiom with the already existing axioms creates a new system.

For example:

Two parallel lines will never intersect each other

This is true when you are in Euclidean Geometry where right angles and plane of paper are of prime importance. Where the plan of paper has no curvature

But when you are able change the curvature of the paper where parallel lines are drawn, you can make them intersect.

The no intersection idea of parallel lines is the basis of Euclidean geometry but their intersection is not provable in the Euclidean geometry itself. You have to create non-Euclidean geometry (Hyperbolic, Elliptical geometry discovered by Lobachevsky and Gauss) in order to prove the point.

This means that the statement that Parallel lines may intersect has to be assumed as true with no proof in Euclidean geometry, once accepted as the truth it developed a new a system called non-Euclidean geometry where the system became more complicated.

This brings us to one final question that- Can we know everything that is there to know in mathematics given that it is the purest form of truth?

And the answer is No.

The Gödel’s incompleteness theorem proves that there always will be some true statements in a system where there will be no proof to prove them true. The acceptance of these statements as true will lead to development of new system.

The challenge for mathematicians is that accepting something to be true without having a proof to call it the truth. If some mathematical statement when tested to be true to every mathematical simulation proves to be true, should we accept it as the unprovable truth?

This highlights the incompleteness of Mathematics.

The Millennium problems and Gödel’s Incompleteness theorem

There are some problems in mathematics famously called as the millennium problems. The problems yet not proved and if proved true will completely revolutionize the mathematics thereby creating a new system of the axioms and their combinations.

The Goldbach conjecture, Riemann Hypothesis, Nature of the roots of the Navier-Stokes Equations are some of them.

The great thing about the Gödel’s Incompleteness theorem is that the idea of numbering the statements led to the development of machine language, programming and developments of early computers.

There is a concept in artificial neural networks called grey box model where you try to predict the outcome of events based on the already fed relations between variables, interactions between them and their outcomes. We actually do not know what is happening inside the grey box models of the neural networks but we know that when fed with enough data the outcomes are true based on real conditions.

The Gödel’s incompleteness also makes us question our biases. If something true is not provable, how would you prove it to be true OR if it’s not provably true is it really true? ( One of the millennium problem possible unprovable known as Fermat’s last theorem is proved after whopping 350 years) This also highlights how difficult it is to develop a purely original mathematical idea, how small amount of time we have as a human to discover the marvels of the nature, universe around us.

The conclusion is that there always will be something that is not complete. There always will be something that we may not know. There always will be something that needs development of new foundations to be true. There always will be something in this universe (and may be multiverse) that still needs to be discovered which will give us new perspective to look at things.

Ignoramus et ignorabimus
we do not know and will not know

Why the philosophical search for the ultimate universal truth is useless?

An Existential Meme Caption and Its Resolution

There Is No Final Truth.

The Münchhausen Trilemma

Resolving the Trilemma

Skepticism, Agrippa and the Suspension of the Judgement

You can share this:

The Spirit of the Void for the modern world

Void and the Incompleteness of the Mathematics

The Void and The Dunning-Kruger Effect

The Void and Ralph Waldo Emerson’s Modern Scholar

The Void and Einstein

The Void and The Quantum Mechanics

Conclusion

– 1 –

– 2 –

– 3 –

You can share this:

Nature of Mathematics

The paradox of self reference in Set theory

The Ignorabimus

The Paradox-

The Millennium problems and Gödel’s Incompleteness theorem

You can share this: