Tag: George Cantor

I remember the times in the school when we were introduced to the proofs of geometric theorems. There was this systematic template that you had to follow to secure full marks for the question. You would write the “Statement of the theorem”. Establish a geometry, define its components called “Drawing”. Then you would write “To prove”. Finally, you would follow the steps, based on the foundations you had in order to develop the final proof- “to prove”. The moment of relief was to rewrite the “to prove” statement again followed by “hence proved”.

Fun part of proving mathematical theorems was that, if one’s proofs were wrong or contained half written answers- he/she would fight for the marks of steps. I remember my friend (that one who used to study for wrong subject on wrong day) who wrote only the statement of theorem followed by “hence proved” or “LHS=RHS” in a (stupid) hope that it will yield at least one mark. Because of these theorems, there were two types of Mathematics teachers- The God mathematics teacher and the Devil mathematics teacher. No need to explain that the God mathematics teacher gave marks for the correct steps irrespective of the final proof. In short, mathematical theorems made us realize that there are some good mathematics teachers too. (a rare species!)

This funny and real experience reveal the true nature of mathematics.

Nature of Mathematics

Mathematics is made up of some systematic and logical steps which will reveal the nature of reality around us. Mathematics is not subjective; it is strong and resourceful to stand for itself. In simple words. Out of all the schools of thoughts mankind has developed, Mathematics is the purest of all. Mathematics never favors a thought just because some king, any political person or any spiritual leader has issued an order to call it true. Any mathematically proven true statement will remain true irrespective of the paths followed to reach it. Hence the reason, mathematics is the reflection of the truth rather the truth itself.       

Mathematics has its own system of truths called “Axioms” and “logic” to decide whether any proposition is true or false. For any “given statement” to be true, there is a systematic approach of questioning the impact of “given statement” on other mathematical system which are already proven to be true. If the already “proven true mathematical systems” still follow their true behavior after involving the “given statement” – the statement is called as true. This is also what can be roughly called as “Consistency”. If given statement is true then it cannot be contradicted.

There is one idea for proving mathematical proofs involving “proof by contradiction”. You assume the proof to be false, then follow the logic and reveal that the outcome does not concur with the what was to be proved hence the assumption that it was false was false; hence whatever was to be proved true is true. Simple example can be given as follows:

One can simply ask some questions to conclude that 1+1=2 is a true statement. In whatever way one will negate the statement, the person will not reach to consistent and fixed result thereby proving the negation false.

From here on, our actual story starts,

The paradox of self reference in Set theory

Set theory is one of the most important (simple and complex simultaneously) in mathematics developed by George Cantor. A set can be collection of anything which follows certain rules. Set of cars will include all the cars you can see, set of planets in the solar system will include all the planets (excluding Pluto!).

What about a set of all sets- The set that contains everything?

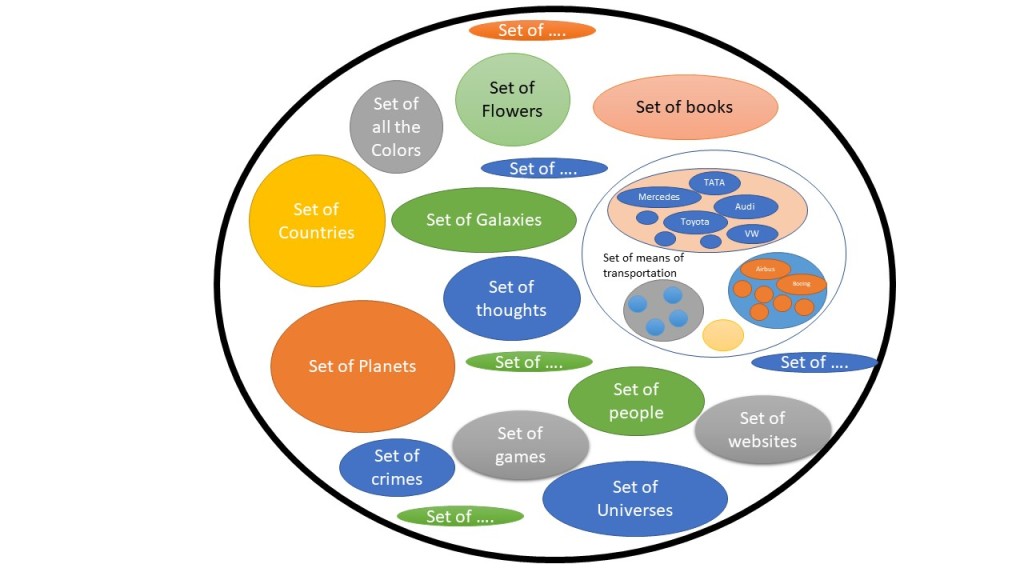
Now the question comes, does the set that contains all sets, contain itself?

If “the set that contains all the sets” does not contain itself then it leaves itself outside of itself- hence it doesn’t become “the set that contains all sets”- but it is “the set that contains all the sets”. This leads to contradiction, famously called as “Self-contradiction”. This was found out by Bertrand Russel.

Here is one more example:

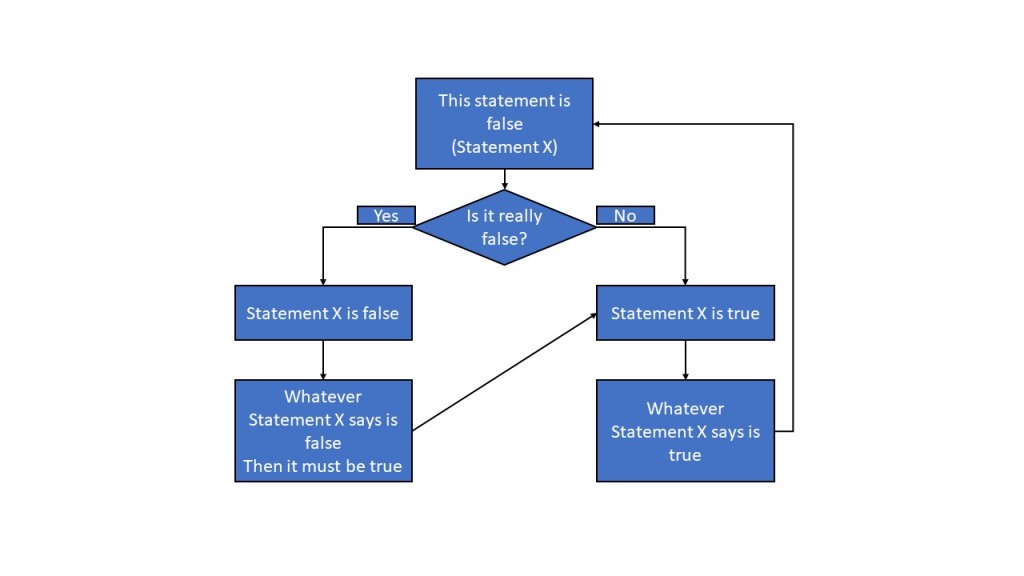
Unlike our previous algorithm to prove 1+1=2, here the algorithm doesn’t break out to either true or false. It contradicts itself to be true or false hence gets in continuous loop. This is where, the mathematicians realized the true boundaries of what we can know and what we cannot know.

The Barber’s Paradox is also one funny example paradox of self-reference.

The two cases of self-contradictions explained above are verbal paradoxes, means that their outcome may be subjective based on what every person understands from the meaning of the words; they can be twisted to any person’s meaning or understanding. Mathematical truths are not like that, they are specific and cannot be twisted to make any desirable or subjective outcome.

The Ignorabimus

Boasting on the strong foundations and objective nature of Mathematics, many mathematicians called mathematics to be consistent thus they began the quest to prove the consistency of the mathematics. One of them was David Hilbert- one of the most influential mathematicians of all times. According to Hilbert, mathematics was consistent meaning for every mathematical true statement there exists no contradiction. It always follows only one single truth and its falsification of this truth does not exist. He had given a famous lecture to deny an idea called “Ignorabimus” (a latin maxim meaning “we will not know”- a topic for new and later discussion) saying that “We can know everything that is there to know and we will know that all”.  

In reality, that was not the case. A day before this lecture actually happened- a logician called Kurt Gödel had proved that mathematics is not consistent. Means, contradictions can happen in mathematics. This was a shock for all the mathematics community. It’s like the truths in mathematics can be twisted to prove any wrong thing right.

Gödel had devised a method (purely mathematical) to prove that mathematics was not consistent.  

It somewhat aligns with the thought process of Self-referential paradox or the paradox of set theory.

Gödel developed a system, this system is well explained elsewhere (find the link in Further readings section):

Gödel defined a number to each logical operator and number like for “and”, “or”, “not”, “successor” (means any number before the number), “addition”, “subtraction” and so on. Based on the statement, take for 1+1=2 he pulled out a mathematical function to give out a number which represents that statement. Similarly for all the axioms, Gödel pulled out these individual numbers. So, when you want to prove that 2+1=3, you will pull a number for that statement. The number pulled out from the expression 2+1=3 will have provable connection with the statement 1+1=2 thereby proving the statement 2+1=3 to be true.   

Gödel developed the numbers for the axioms and proved that any statements can be proved from the operations on the numerical representatives of the statement to be proved.

For example:

When we enter 1+1=2 in a computer, the computer assigns the number and operator a unique code in 1s and 0s also known as ASCII (American Standard Code for Information Interchange) uses somewhat same idea to solve the addition operations to give output in a number containing 1s and 0s then converting it to the output display of calculator.

The fun starts when Gödel purely mathematically formulated number for a statement which was Self-referential paradox. The statement was like this:

“There is no proof for the statement with Gödel number g”

Meaning, that there exists no proof for the statement which number g indicates in the system out of which it has been created. The statement is unprovable

The Paradox-

There are two cases to be evaluated:

1. If the above Gödel statement is false means, there is a proof. But according to Gödel statement there is no proof in the system Gödel created, thereby creating a contradiction.
2. If the above Gödel statement is true means it is not provable from the Gödel system.

Either of the cases evaluated above lead us to conclude that the current system in which the statement was created will not have the proof for some true statements thus making it incomplete.

You will need to jump out of the system to create a new proof to evaluate the truth of the system because given system has insufficient axioms to prove the new statement to be true, hence the new statement itself becomes a new axiom.

The combination of this axiom with the already existing axioms creates a new system.

For example:

Two parallel lines will never intersect each other

This is true when you are in Euclidean Geometry where right angles and plane of paper are of prime importance. Where the plan of paper has no curvature

But when you are able change the curvature of the paper where parallel lines are drawn, you can make them intersect.

The no intersection idea of parallel lines is the basis of Euclidean geometry but their intersection is not provable in the Euclidean geometry itself. You have to create non-Euclidean geometry (Hyperbolic, Elliptical geometry discovered by Lobachevsky and Gauss) in order to prove the point.

This means that the statement that Parallel lines may intersect has to be assumed as true with no proof in Euclidean geometry, once accepted as the truth it developed a new a system called non-Euclidean geometry where the system became more complicated.

This brings us to one final question that- Can we know everything that is there to know in mathematics given that it is the purest form of truth?

And the answer is No.

The Gödel’s incompleteness theorem proves that there always will be some true statements in a system where there will be no proof to prove them true. The acceptance of these statements as true will lead to development of new system.

The challenge for mathematicians is that accepting something to be true without having a proof to call it the truth. If some mathematical statement when tested to be true to every mathematical simulation proves to be true, should we accept it as the unprovable truth?

This highlights the incompleteness of Mathematics.

The Millennium problems and Gödel’s Incompleteness theorem

There are some problems in mathematics famously called as the millennium problems. The problems yet not proved and if proved true will completely revolutionize the mathematics thereby creating a new system of the axioms and their combinations.

The Goldbach conjecture, Riemann Hypothesis, Nature of the roots of the Navier-Stokes Equations are some of them.

The great thing about the Gödel’s Incompleteness theorem is that the idea of numbering the statements led to the development of machine language, programming and developments of early computers.

There is a concept in artificial neural networks called grey box model where you try to predict the outcome of events based on the already fed relations between variables, interactions between them and their outcomes. We actually do not know what is happening inside the grey box models of the neural networks but we know that when fed with enough data the outcomes are true based on real conditions.

The Gödel’s incompleteness also makes us question our biases. If something true is not provable, how would you prove it to be true OR if it’s not provably true is it really true? ( One of the millennium problem possible unprovable known as Fermat’s last theorem is proved after whopping 350 years) This also highlights how difficult it is to develop a purely original mathematical idea, how small amount of time we have as a human to discover the marvels of the nature, universe around us.

The conclusion is that there always will be something that is not complete. There always will be something that we may not know. There always will be something that needs development of new foundations to be true. There always will be something in this universe (and may be multiverse) that still needs to be discovered which will give us new perspective to look at things.

Ignoramus et ignorabimus

we do not know and will not know

Further reading:

1. How Gödel’s Proof Works– Quanta Magazine
2. George Cantor– Wikipedia
3. Bertrand Russel– Wikipedia
4. David Hilbert– Wikipedia
5. Kurt Gödel– Wikipedia
6. Fermat’s Last theorem– Wikipedia
7. Millennium Problems-Clay Mathematics Institute
8. The Barber’s Paradox– Wikipedia