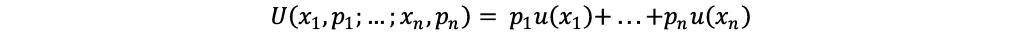Tag: Finance

Settling accounts with the losses

Why do we get so confused while selecting the best smartphone model and end up selecting high-costing ones? Why do people still fall for easy money schemes, Ponzi schemes, Pyramid schemes even though they are well informed about similar fraud cases? Why most of the people are ready to buy a million-dollar lottery ticket costing few pennies even when they know that the chances are very low? Why do people fall in the spiral of gambling even when they have hit the rock bottom of debts? Why retail investors are continuously losing huge amount of money in stock market when they know that it is a loss-making venture? What convinces them to continue further? Why people always lookout for complete cover while selecting insurance policies even when they know that chances of those problems are really low? Prospect theory has answers to these questions.
Daniel Kahneman and Amos Tversky’s Prospect theory shows certain behavioral effects called certainty effect, reflection effect and isolation effect while making economics related decisions. Prospect theory explains why people love certain but smaller gains and also why same people will turn into complete gamblers in a crisis situation.

Daniel Kahneman and Amos Tversky’s Prospect theory in economics

Prospect theory is one of the most important ideas of behavioral economics. It shows how people make choices when times are highly uncertain. Rationally, any person would go with the choices having the best probable outcomes in uncertain times but in real scenarios that is not the case. Real people are emotional and always have mindset of survival. That is exactly why in uncertain times, people choose anything that has complete surety, certainty of gain instead of gambling for higher gains however highly probable they may be. And when probable gains are very high than average gains people will choose higher gains even when they have very less probability. This irrational, non-economical behavior may make human decision seem illogical, inconsistent. This illogical behavior is an important part of our evolution as species which Nobel Laureate Daniel Kahneman’s Prospect theory highlights. We will throw more light on prospect theory hereon.       

Expected Utility Theory

“The agent of economic theory is rational, selfish, and his tastes do not change.”

Expected utility theory lies at the foundations of economics. It allows economists to model the scenarios to understand the dynamics between the resources, their perceived value and the risks/ uncertainties involved in any transaction.

The basic idea behind expected utility theory is that for any given set of uncertain events, a rational agent considers the weighted average of all gains based on the probabilities. The rational agent makes decision based on overall gains rather than being biased towards certain high value gains or certain highly probable gains.

For those who want more details, I have written in depth on the expected utility theory.  

Prospect Theory

Although expected utility is one of the fundamental concepts of economics, the assumptions on which it stands have their own limitations. So, expected utility theory is not a complete and absolute theory to understand and predict the behavior of agents in economics. The moment we are injecting the word “behavior” we must understand that humans are not a purely mechanical or mathematical thinkers – decision makers. Also, as per the expected utility theory, there can be different perception of the value for given same resource for different agents. What expected utility immediately does is to fully attach the perception of value of given gain only with the bulk of resource that agent already has and the value addition it would do to this already existing bunch of resource. There is no psychological element in this discussion which is a larger predictor of the behavior of the agents in economics.

So, you can call prospect theory as an augmentation of expected utility theory. Prospect theory is not meant to falsify the expected utility theory rather it helps EUT to evolve where its own assumptions fail to explain the behavioral decision of the agents.

Modern economists are making more efforts to incorporate the psychological aspects of decision making into the machine-like purely mathematical models of economics. This makes the predictions more realistic when human decision making is involved. Daniel Kahneman and Amos Tversky published their world-famous paper called ‘Prospect theory: An analysis of decision under risk’ in ‘Econometrica’ in 1979. This paper is one of the most cited papers in economics. Prospect theory thus became the cornerstone of behavioral economics.

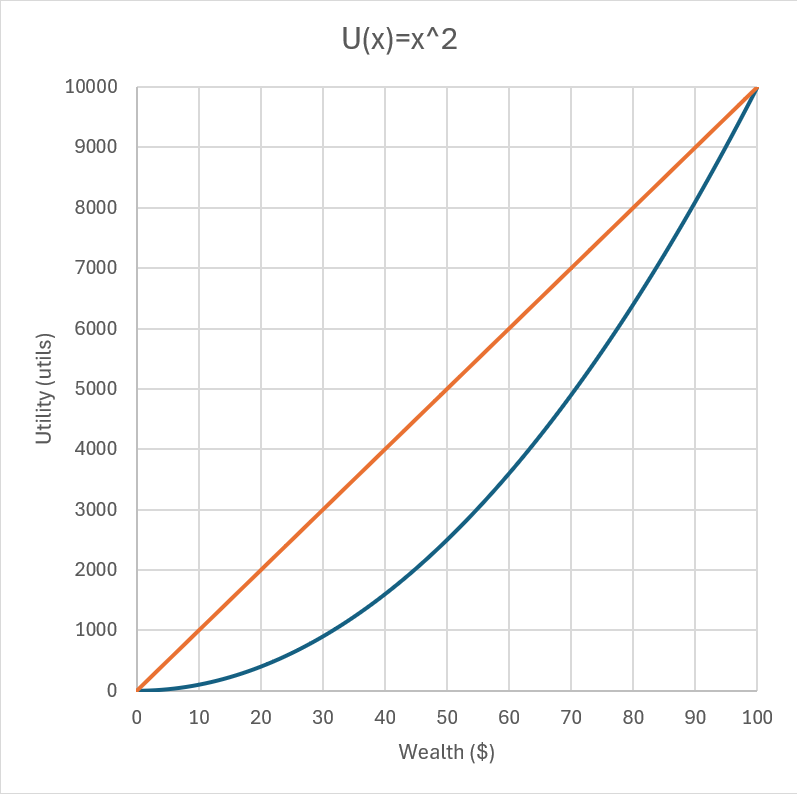
Kahneman and Tversky pointed out one “theoretical blindness” imparted due to the EUT. We will see those details in depth. They pointed out certain effects based on the decision making of the subjects under different decision-making events. Collection of these effects makes the prospect theory important. The important point to keep in mind is that everyone is risk averse in reality. Nobody wants to choose the transaction where there expected utility is reduced. So, the utility function of agents is concave. 

Certainty effect

People overweight outcomes that are considered certain, relative to outcomes which are merely probable.

According to EUT, people will weigh out the outcomes based on their probabilities, but Kahneman-Tversky found out that people love certainty of gains. People don’t want to get involved into gambles when they know that there another way to gain something “closely valuable” for sure.

Kahneman-Tversky presented an interesting observation in their paper, here are the exact scenarios:

Choose between

A:            Gain of 2500 with probability 0.33

                Gain of 2400 with probability 0.66

                Gain of 0 with probability 0.01

OR

B:            Gain of 2400 with certainty

According to the EUT the utility equivalent of A can be calculated as

U(A) = (2500 x 0.33) + (2400 x 0.66) + (0 x 0.01) = 2409

And utility equivalent of B

U(B) = (2400 x 1) =2400

So, according to EUT the utility of A is higher than B. But you already have your answer ready in your mind. Same was observed by Kahneman- Tversky; 82% of the people choose event B where the gain was certain.

Does this mean that the more probable the gain the more preferred it will be?

The answer is complicated.

Kahneman- Tversky further posed a modified event,

Choose between

C:            Gain of 2500 with probability 0.33

                Gain of 0 with probability 0.67

OR

D:            Gain of 2400 with probability 0.34

                Gain of 0 with probability 0.66

They observed that 83% of the people chose event C over event D. This was surprising because event D is mathematically more significant (probability of 0.34 in D over 0.33 in C). This shows that it’s not just about the higher certainty which drives the preferences. The moment given options are uncertain people rarely notice the extent of the uncertainty (numerical value of probability) to choose between.

Take one more example given by Kahneman-Tversky

A:            Gain of 4000 with probability 0.80

OR

B:            Gain of 3000 for sure

Here 80% of people chose B.

But when presented following:

C:            Gain of 4000 with probability 0.20

OR

D:            Gain of 3000 with probability 0.25

Here 65% people chose C.

What exactly is happening here?

People love sure gains over any uncertain gains. But when both or all of the presented gains are uncertain, people will choose to gamble with those giving higher gain, whatever may be the possibility. This goes against EUT which says rational people would consider both the gain and the probability while making a decision. In reality when people are uncertain, they choose to go with the uncertain but higher chances of gaining.

You will now start to notice that EUT creates an objectivity in the choices by mathematically connecting the gains with their probability. But Kahneman-Tversky observed that real people will not follow EUT, they will make decisions based on the prospects they are presented. People never look at the scenarios in economics as distinct events, they look at the current trade-offs, current prospects they a have at their disposal to choose. The choice is always relative to the prospects presented and not absolute like EUT asks for in a mathematical form. That is exactly why Prospect Theory becomes important. It’s neither about the certainty nor the value, its more about what type of options – prospects you are providing to the people.

This is one important idea in marketing. We will see that in detail as the discussion evolves.

There is an interesting observation by Kahneman-Tversky when we are observing relativity of the prospects:

Choose between

A:            Gain of 6000 with probability of 0.45

OR

B:            Gain of 3000 with probability of 0.90

86% of the people chose prospect B.

If you use EUT, both prospects have same utility equivalent = (6000 x 0.45) = (3000 x 0.9) = 2700.

But people refuse to be indifferent to these prospects and choose the most certain prospect.

Now, one more – same gains but totally different probabilities,

Choose between

A:            Gain of 6000 with probability of 0.001

OR

B:            Gain of 3000 with probability of 0.002

Here, 73% of the people chose prospect A.

Again, both have same utility equivalent = (6000 x 0.001) = (3000 x 0.002) = 6. According to EUT people should be indifferent to both prospects.

And interestingly they didn’t go with the one which is more certain than other. They went the one with larger gain. This is because both prospects have very slim chances of gains.

Now it should be pretty clear that people compare prospects based on what is presented to them. Even when they are risk aversive, they would prefer bigger gambles when they realize that the chances of winning are really low and there is pretty much nothing to lose.

Reflection Effect

The risk aversion in the positive domain is accompanied by risk seeking in the negative domain

Certainty increases the aversiveness of losses as well as desirability of gains.

We saw how people choose when they have information of higher certainty or higher gains. What would happen if we inform them about lower certainty or lower gains/ higher losses?

We already saw one observation from Kahneman-Tversky:

A:            Gain of 4000 with probability 0.80

OR

B:            Gain of 3000 for sure

80% of people chose B because they preferred surety of gain.

Kahneman-Tversky posed exact negative of this prospect which looks like

A:            Loss of 4000 with probability 0.80

OR

B:            Loss of 3000 for sure

Now, 92% of the people chose option A. They don’t want a prospect where loss is certain.

Kahneman-Tversky observed that when prospects are negated people switched sides. The risk aversion in positive prospects changed to risk seeking which goes against EUT. They called it the reflection effect.

See this already discussed prospect:

Choose between

A:            Gain of 6000 with probability of 0.001

OR

B:            Gain of 3000 with probability of  

73% of the people chose prospect A.

The negative of this would be:

Choose between

A:            Loss of 6000 with probability of 0.001

OR

B:            Loss of 3000 with probability of 0.002

Kahneman-Tversky observed that 70% of the people chose prospect B.

When it came to losses, people chose prospect with more certainty of lower loss.

This is very interesting observation. If you still cannot wrap your mind around this, the simplification looks like this: People rarely care about the combined effect of gains/losses with the probabilities as the expected utility theory rationally establishes. People care about what current choices they have and choose those which guarantee highly certain gains even when they are low and choose lower losses when they are highly certain.

“…it appears that certainty increases the aversiveness of losses as well as the desirability of gains”   

Isolation effect

In order to simplify the choices between alternatives, people often disregard components that the alternatives share, and focus on the components that distinguish them.

The core of this idea is that people don’t like complexity or our brain is always trying to take shortcuts. This is one important idea and observation on human nature which Kahneman-Tversky pointed out.

What they did is creating a two-stage game:

 1st Stage-

P:            Gain of 0 with probability of 0.75

OR

Q:           Move to 2nd stage of the game with probability of 0.25

2nd Stage-

R:            Gain of 4000 with probability of 0.8

OR

S:            Gain of 3000 for certainty

The condition here is that choices must be made before the game is played i.e., before the actual outcome becomes apparent.

  Before we go to what Kahneman-Tversky observed. Let us see what EUT would prefer, what a rational person would prefer:

U(R) = The equivalent utility of gaining 4000 at the end of the game = 4000 x (probability of reaching 2nd stage from 1st stage) x (probability of gain of 4000) = 4000 x 0.25 x 0.8 = 800

U(S) = The equivalent utility of gaining 3000 at the end of the game = 3000 x (probability of reaching 2nd stage from 1st stage) x (probability of gain of 3000) = 3000 x 0.25 x 1 = 750

So, U(R) > U(S). Thus, any rational person would choose prospect R in any situation as per the EUT goes.

Pay attention here,

The added complexity due to multiple stages –

When people were presented with the above mentioned two stage scenarios, 78% of the people chose the prospect giving certain gain i.e., gain of 3000 for sure. But, according to EUT you will see that this chosen prospect has lover equivalent utility. People actually ignored (or didn’t account for) the effect of the first stage of probability which would allow them to enter the actual stage 2.

Kahneman-Tversky called this an Isolation effect where people isolate or don’t care the commonalities between presented scenarios to make the decision-making process less complicated.

Now, this 2-stage game can be reduced to single stage game as follows:

Choose between

A:            Coming to current stage with 0.25 chance where there is 0.8 chance to gain 4000

                (0.25 x 0.8) chance to gain 4000

Gain of 4000 with probability of 0.20

OR

B:            Coming to current stage with 0.25 chance where there is certainty to gain 3000

                (0.25 x 1) chance to gain 3000

Gain of 3000 with probability of 0.25

This is a reduced form of the prospect.

If EUT is applied here

U(A) = 4000 x 0.20 = 800 and U(B) = 3000 x 0.25 = 750.

The 2-stage game and its reduced form obviously will have exactly same equivalent utilities because the reduced form just combines the chances of two stages into one resultant number. So, even though these two scenarios have same outcomes of equivalent utilities, Kahneman- Tversky observed that the ways in which these scenarios are presented affect the choices of the people.

Kahneman-Tversky had already observed that when there is significantly less difference in the amounts of gains or the probability of those respective gains in two prospects, people mostly prefer the one with higher gains. So, if we present this above mentioned 2-stage scenario to its reduced single stage scenario the results are interesting. 

We have already seen what Kahneman-Tversky observed for this reduced scenario. Majority of people chose higher gain prospect even though it was relatively less probable.

Conclusion

What Kahneman-Tversky did concretely in prospect theory is to formulate the value function to mathematically explain this behavior.

The value function in prospect theory is given as follows:

The simplified idea of this value function is:

The pain of losing certain amount hurts us more that the joy of gaining the same amount.   

You just like winning and dislike losing – and you almost certainly dislike losing more than you like winning.

The importance of prospect theory is that it shows what it means to be a human. Once you start collecting the pieces of certainty effect, reflection effect and isolation effect the picture that is revealed is profound insight about our tendencies to ensure survival in any case.

Certainty effect shows that people will choose certain gains even if their size is low. They just want to be at peace with increasing their existing surplus if it is sure.

This is how the coupon codes, vouchers, discount codes, discount days work in online shopping. The provider lures you into buying something you really don’t want by giving you guarantee, surety that you surely are making profit out of this deal. One smart thing that happens here is that the sense of urgency. You might have realized that these coupons are expiring immediately like virtually now. This creates an urgency to materialize the profit.

When people are in profit making environment, they will always prefer sure profit over uncertain profits and that is exactly how scammers lure people. They create this sense of surety to attract people to invest in their schemes.

No wonder why people love easy money. Once you inject the surety of gains in any venture people will literally pile up and that is how Ponzi schemes, Pyramid schemes work.     

The moment this surety of gain is lost and when people realize that it is only the losses that they will have to face then immediately this same population craves for uncertainty in the losses. When people see that they anyways have to digest the losses they avoid certain losses over uncertain ones, even if the actual effect of certain losses was pretty low. This is reflection effect.

The stock market is the best example to explain the reflection effect. In the crisis times – bearish markets, history has evidences that people have gone with insanely foolish bets where chances of gains are slim to none. People end up in the cycles of betting, gambling even when the realistic indicators of market are pointing to inevitable crisis.

The important thing to appreciate from prospect theory is to know when and where to stop in crisis situations.

“…people become risk seeking when all their options are bad”

If you have lost this game in poker or any gamble, you always feel that I will play the next game and definitely (somehow) will recover my losses (even when I know that James Bond is sitting on my table).

You will be more relaxed if you were told in advance that you will make less money of $10000 and you will be more stressed, feel pain if you make $12000 and government cuts $2000 for some taxation at the last moment. The gain is same but the “prospects” are different.

People can be confused to choose the loss-making options even when they are completely informed. When decision making is multi-stage so that there are some common things between them, people usually neglect those shared attributes even if they are significant and move on to the differences to finalize the choice even if these differences are not significant. This is isolation effect.

Many electronics companies while creating their pricing strategies intentionally create shared features and smartly just add one low-cost additional feature in the top model to sell it at foolishly, unjustifiably higher cost. People are ready to pay higher prices for that low cost (for the manufacturer/ marketeer) because it makes that model better. (You know who I am talking about.)

For me, the isolation effect has a huge philosophical implication.

Kahneman-Tversky have attributed the behaviors pointed out by Prospect theory to the tendency for survival. If you want to survive and are living in an already good situation then you would not want to disturb the current resources you have, that is why you don’t prefer uncertain gains, you are more than happy if the gains are certain even if they are small in size because they are not disturbing the already materialized gains.

In same way when conditions to survive are hostile you would take that every chance to increase your resources, however slim the chances may be. This is some kind of indication of hope. Important thing about Prospect theory is that Kahneman-Tversky pointed out that this exact risk-taking tendency in negative environment can push people into the spiral of continuous losses.    

We are naturally evolved in this way. 

The isolation effect outlines our tendency to eliminate common/ shared attributes of given resource to make a choice. The key thing to appreciate here is that while neglecting these commonalities we are never conscious of how significant they are in our life. You must appreciate that when I am writing this, sharing this, when you are reading this, we have more than enough resources to sustain a basic life. We are living better life than most of the world population but still we are not satisfied because we have already isolated that which we have with us. The isolation effect thus points out to our tendency to lose the feeling of gratitude for everything we have right now.

We rarely appreciate things which we already have or things we are sure that we would never loose. Many times, people realize the worth of things as really significant – as truly valuable when they are lost. 

Being alive and having the ability to experience – to appreciate this life is what common to all of us, this is precious than anything else in this world, rest is just the bonus. We should not let the practice of comparison isolate this preciousness.

References and further reading:

  1. Kahneman, Daniel., and Amos Tversky. “Prospect theory: An analysis of decision under risk.” Econometrica 47.2 (1979): 363-391
  2. Thinking fast and slow – Daniel Kahneman
  3. Risk and Rationality in Uncertainty – On Expected Utility Theory
  4. Connecting money with sentiments – Behavioral Economics

Risk and Rationality in Uncertainty

We have many philosophical ideas about how money is not everything in life but deep down, everyone knows how money constitutes to a bigger portion of who we are. Although money can’t buy everything, the unexplainable value it holds behind presence of almost everything in our lives will never go unnoticed. We know that this importance of money/ resources/ assets is highly dependent on how much of those we have right now and how much of those may get lost in an uncertain event. This perception of value drives our decision making in risky situations. The Expected Utility Theory (EUT) in economics deals with the modelling of such scenarios. The mathematical formalization of the perception of wealth and our risk profile is facilitated by this fundamental theory. EUT lies at the foundation of actuarial science/ insurance, financial risk management, decision making under budget restrictions, asset management, and investment management.

EXPECTED UTILITY THEORY

We live in an uncertain world. Timing events where too many interactions are happening could be risky especially when it comes to money or the basic resources for sustenance. In crisis situations, our survival instincts have always kicked in to ensure preservation of life and the resources required to ensure its longevity. They need not to be always rational, they are just meant to save life somehow, that is why most of the acts of survival seem extraordinary. Interesting thing to understand here is that when such extraordinary survival instincts kick in as a mass effect the whole mass effect becomes irrational, unexplainable, incoherent. There is no sane explanation to justify these mass events. When such events badly affect the resources responsible for basic life of every being, it can be catastrophic. Huge sudden falls in stock market are good indicators of such disasters, crises. Insurance on the other hand could prepare person to handle the disasters in a preventive way. Stock market and insurance are one of the best examples to understand how people assess risk and maintain/ reject rationality while making important decisions. We will see what formal ideas from economics lie behind these events of uncertainty.

Expected Utility Theory (EUT) in Economics

Expected utility theory lays the foundation of how a rational person would make decision in an uncertainty where valuable resources like money are involved. The whole idea is based on the quantification of that uncertainty and connecting that uncertainty with the individual gains from individual uncertain event. Expected utility also creates a formal structure of how person perceives risk in given scenario. This helps to quantify the value generated from any economic event.

Origin – St. Petersburg Paradox

Daniel Bernoulli is credited to establish the expected utility theory which is one of the foundations of economics. The theory emerged from the St. Petersburg Paradox which goes like this:

You have $2 and we toss a coin. Heads, the amount you have now is doubled and tails then the game stops and you leave with whatever amount you have right now. The game continues till its always heads in series and stops when the coin shows tails.

The question is how much will you be willing to pay to enter this bet?

The probability of heads and tails is 50-50% which is ½ . If it is a series of heads (heads followed by heads) then the events are dependent on each other, so the probability of this event is intertwined with the probability of the previous one. If there happens a game where you start with $2 and every time heads comes, and the money goes on doubling the equation of gain would be:

As this math goes, a person should pay infinite amount as he will be gaining infinite amount from such game. ‘E’ value here is identified as expected value. Even if one such possible game would happen in reality, people won’t pay infinite amount in reality to enter this bet. 

Bernoulli resolved this paradox by creating the concept of Expected utility. People will pay not what actual value it delivers (as in the $s of money); they will pay according to how actually it will be useful to them, ‘utilizable’ to them – that is where the utility and thus expected utility comes in picture.

Expected utility is calculated by the amount one would gain and the chances of gaining that amount. The expected utility thus is sum of all the gains connected with the probabilities of gaining them.

Daniel Bernoulli
The determination of the value of an item must not be based on its price, but rather on the utility it yields.

1st Tenet of EUT: Expectation

The overall utility of a prospect, is the expected utility of its outcomes.

In very simple words, for a given scenario you will weigh the chances of its constituent events and connect them with their respective gains. The sum of the all connections of each gain with their chance of realization is the usefulness – utility of that scenario.

Mathematically,

Expectation:

In our example we need to assume something that is the usability of the money – utility.

We assume $10 has utility of 1 unit. (This is just an assumption to understand the concept. When multiple objects are involved, their utilities will be different.)

So, the expected utility of this scenario is:

E = ((1000/10)x0.2) + ((50/10)x0.65) + (10000)x0.15) =

20 + 3.25 + 150 = 173.25 units

So, the expected utility – the usefulness of this event is 173.25 units.

The unit of value which we assumed in this calculation is sometimes called ‘utils’ – the basic unit of utility. It will change based on how one perceives the value in given scenario. 

You will realize that the expected utility is the weighted average of utility of events and their individual probabilities.

Four Axioms of Utility Theory

Later John von Neumann and Oskar Morgenstern expanded the concept of EUT with the idea of rationality. The agents involved in such uncertain economic exchanges are ‘econs’-the rational beings.

Oskar Morgenstern & John von Neumann

They have clear preferences among the options provided in every economic decision which comes under the idea of “completeness”. If out of the given set they select multiple options at a time, then it is said that they are ‘indifferent’ to these options. Whatever might be the internal distribution of constituent they might have. It’s about the final utility they perceive. When presented with choices, a rational person has clear preferences for those choices.

For all given uncertain events there is a hierarchy of preferences. If A is preferred over B and B is preferred over C, then A is always preferred over C. Which goes as transitivity.

Suppose we have been presented three events where event A is preferred over B and B is preferred over C. Now if one introduces a new event N which is slightly less preferred than B and more preferred over C then event B and N would be indifferent. In simple words, the choices between options would never directly jump, they will align as per the preferences in line.

So, A>B>C and B>N>C then A>B>C and A>N>C mean the same.

This is continuity. Graphically, the utility function is always a smooth curve.

Why do A>B>C and A>N>C mean the same even when the calculated numeric value would differ? It is because utility is never an absolute value it is just used to arrange the preferences by quantifying them. Ground rules used to define usability from the given resources i.e., the utility function of given scenario will be different for different scenarios and different sets of people. This is simplification of the concept called ordinality of utility. You can rank utility but not say that event A is this many percent better than event B.

When you have set the preferences of A over B and if you are offered another totally different/ irrelevant event M with new utility. You would still prefer A over B. Introduction of M will not affect the preferences as if A and B are independent of M. This is called ‘independence‘ in EUT.

So, completeness, transitivity, continuity and independence are the four axioms of EUT. Note that they are not ‘complete’ representation of reality. It’s just that they bring in simplicity to treat given scenarios and evaluate them. That is why you will find contradictions to these axioms. (Maybe a topic for another time.) The axioms are there to create a formal mathematical structure to draw useful inferences.  

2nd Tenet of Expected Utility Theory: Asset Integration

In EUT, asset integration is an idea based on the assumption that all people making economic decisions are rational. So, in uncertainty or risky scenarios a rational person will look at the overall gains instead of focusing on one certain gain and neglecting other unsure gains. A rational person will look at the risks of scenarios in a collective way and decide to enter only if the expected utility improves his assets’ position. A rational person will only enter the given scenario if the collective utility is better than the individual utility of its sub-events or sub-gains.

A rational person will not focus on an individual more probable gain even when his overall gains are becoming low.  

3rd Tenet of Expected Utility Theory: Risk

The beautiful insight EUT creates is about the mathematical formalization of risk profile. For that we will understand some ideas in advance.

Utility function – it is a mathematical relation between how one sees the value of given object/ resource. The value of resources is different for different people. A crude example would be how a beggar values money for one time meal compared to a filthy rich person. The value of $25 would be different for different people based on the conditions they are in.

This is where marginal utility comes in picture.

Marginal utility talks about what difference it makes in your perception of the value of a given thing if one would give you more of that in the next event. Roughly speaking the more we have something, the less we value it, so marginal utility is always diminishing. If I already have 10 packets of chocolates which are enough for the day to me, the next 11th packet of chocolate won’t make that much difference in my current excitement of having 10 packets. (Please note that we are talking about rationality here, although nobody is rational when it comes to chocolates.) A rational version of me would trade that 11th packet for something else with a person who hasn’t received even a single packet. A person who has no chocolate would perceive that single packet with higher value than how I perceived it (provided that he loves chocolates).

Alfred Marshall – the British Economist brought the concept of
‘Marginal Utility’ through his book ‘Principles of Economics’ in 1890.

So, utility function is a mathematical transformation of objects in given event to a unitary value so that the results can be easily compared with each other because the transformation converts everything to single unit system. These single unit of value is called ‘util’.

Utility function can be any possible mathematical relation. Generally, it is expected to be simple to not invite the complexities in modeling of given economic scenario. It should be simple enough to draw realistic conclusions.

An understanding of utility function gives insight into how the person evaluates risk with respect to the resources they hold.

Consider a scenario:

Event 1 – You enter a lottery where there is 50% chance that you will win $100 and 50% chance that you win nothing.

Event 2 – You are given $50 for sure, unconditionally just for playing the lottery.

Assume we have three differently thinking people to make choices in this scenario. Different thinking means how they assess the risk of entering the lottery which has some uncertainty and the surety of winning $50. Difference in assessment of risk means difference in the perception of utility. It further means that the utility function will be characteristic to each person.

Person 1 has the following utility function:

So, for Person 1 the utility of certainty (7.07 utils) is higher than the uncertainty (5 utils). He is happy to walk away with sure $50 gain instead of betting for $100 lottery.

Person 1 doesn’t want to take risk by entering the Event 1 of betting when he is sure about gain of $50 in Event 2. This is risk-averse behavior. The utility function mathematically models that risk averse behavior. Utility function is concave in risk aversion.

Now comes Person 2 with the following utility function:

You will see that the utility of certain and uncertain choices is the same. It means that it doesn’t matter for this guy if he enters the lottery having uncertainty or gets $50 for sure. This is risk-neutral behavior. The person 2 doesn’t care about certainty or uncertainty. He values both events the same. As mathematically both have similar utilities. Person 2 is indifferent to both events.

Now see the Person 3 with following utility function:

This guy has a radical view, he perceives the worth of entering the lottery (5000 utils) better than gaining $50 for sure (2500 utils). This guy is gambler! He finds it more interesting to enter the bet instead of gaining $50 for sure. He is happy to take the risk in uncertainty.

Looking at these three people you should note that the scenarios/ events they are presented are exactly the same. The only thing which is different is how they see the value in lottery and the sure gain.

So, the first person demonstrates risk averse behavior. He wants surety of gain rather than gambling for higher but unsure gain.

The second person demonstrates risk neutral behavior. Bet or no bet he doesn’t care. Just be done with it.

The third person demonstrates risk loving behavior. He wants the thrill of uncertainty in betting, so he sees more value in uncertainty of lottery.

This is how Expected Utility Theory can be implemented to mathematically model how different sets of people/fund managers will make decisions based on the risk profile. The relation between expected utility (which is the weighted average of gains) and utility function (which shows how one values the gain) can show us the risk profile.

Risk Averse Utility Function
Risk Neutral Utility Function
Risk Loving Utility Function

In the graphs shown, blue lines show utility function and the orange lines show expected utility. The orange line in our case connects the utility of $100 and $0 which is Event 1. This orange line connects any points on utility curve and it will give the expected utility value for that scenario of uncertain gain. In simple words, it’s the line of weighted average exactly like the definition of expected utility. This line is used to find out the certainty equivalent (CE). A certainty equivalent is the utility of an uncertain gain if it was certain.  

Almost all the time, people are risk averse. People want to avoid uncertainty about higher gains when they are presented with some lower but sure gain. This is where marginal utility becomes important. (This point deserves broad explanation which we will cover another time under Prospect Theory)

Marginal Utility

In risk averse people, you will see that the utility function starts to flatten out once the value gained increases. The more value someone already has the less he values the next addition of bunch into the preexisting bulk. Remember the chocolate box example?

One with 10 boxes of chocolate perceives one additional box with less value, whereas some with no chocolate will see it as a precious one as he has nothing right now. The perceived value of the additional next lot goes on reducing. This is known as diminishing marginal utility. Marginal utility is always diminishing.

So, a safe playing person would stop entering the next gamble because he now has enough. The next uncertainty in gambling has less value for him.

EUT in actuarial

Now it is obvious that only a risk averse person would go for conservative approach in uncertainty. This also means that risk aversion will also invite preventive measure against loss of certain assets, resources. Insurance thus comes into the picture. EUT here helps to mathematically formalize the probability of the risks which would compromise current gains, the perceived value of asset/ property/ resource and losses one can bear. We can now calculate the premium for the insurance against uncertainty of loss of something.

So, we will look into a scenario where risk aversion exists thus marginal utility is always diminishing.

We have the utility function of a man has a property giving revenue of $100K/year as:

u(x)=ln x

Now will see the risk scenario. Suppose this person does a fire audit of his property and the auditing agency finds out that there is 50% chance that he will suffer a loss of $60K/year due to fire hazard and 50% chance that nothing will happen.

After rephrasing, the gains from the property would look this:

50% chance that the income is $40K/year and 50% chance that income is $100K/ year.

Using the tenets of EUT the mathematical expression becomes:

Now, what we are doing differently here is to find out what this expected utility in uncertainty means when there is complete effect of loss with some chance and gain of some chance. In earlier examples we had second event of certainty against which we compared to understand the risk profile. Now it’s reverse calculation, we know the risk profile, we know the perceived overall value i.e., EUT of the property. Now we will find the certainty equivalent (CE) using the risk profile which can be explained by the utility function of the person.

How much is this 11.05 utils in terms of money from the property for this guy? We can find this from utility function of the person.

ln(x)=11.05, thus x=$63245.55

Now, think the fire hazard as a lottery where you gain $63245.55 money as per EUT calculation. Whether the fire will happen or not, the possible overall earning from this property would be $63245.55.

Now, if the property without any fire hazard was giving me $100k and the insurer guarantees me that same earning for the losses due to hazard. How much maximum amount should I pay to the insurance agency?

I will pay only that much amount which falls short to the $100k when compared to perceived earning calculated from the combined effect of certainty and uncertainty as given by EUT.

My earing due to uncertainty is $63.2k/year, I would receive $100 for a fine year so in order to continue that $100k even for a worse year I would pay insurance agency = $100000 – $63245 = $36754.45.

Anything I am paying above $36754.45/ year for insurance premium is loss for me. I would not go above this amount to insure my property which guarantees income of $100k per year. This is how the insurance premium is decided.

Conclusion:

We have many philosophical ideas about how money is not everything in life but deep down everyone knows that money constitutes a bigger portion of who we are. Although money can’t buy everything, the unexplainable value it holds behind presence of almost everything in our lives will never go unnoticed. We know that this importance of money/ resources/ assets is highly dependent on how much of these we have right now and how much of those may get lost. This perception of value drives our decision making in risky situations. The mathematical formalization of the perception of wealth, our risk profile is facilitated by expected utility theory. Although this theory has its own limitations it lies at the foundation of the economics.

For further reading:

  1. Von Neumann, John, and Oskar Morgenstern. “Theory of games and economic behavior: 60th anniversary commemorative edition.” Theory of games and economic behavior. Princeton university press, 2007
  2. Kahneman, Daniel., and Amos Tversky. “Prospect theory: An analysis of decision under risk.” Econometrica 47.2 (1979): 363-391
  3. Thinking fast and slow – Daniel Kahneman
  4. Connecting money with sentiments – Behavioral Economics
  5. Settling accounts with the losses – On Prospect Theory

A Hindsight For Better Future

Morgan Housel – the famous author of ‘The Psychology of Money’ has another important book called “Same as Ever” which gives insight into things which have never changed over the course of time. Same as Ever drives the motto of objective flexibility and subjective awareness of every event happening around us and with us. It also highlights that our mind is the first and the easiest one to fool, which leads to false sense of superiority over others and creates biases. Once we accept that nothing is perfect, no one is perfect – it injects humility and forgiveness. It also makes us to be grateful for what we possess today. The ability to see every event at the same level is a superpower any one of us can have.

An important book from Morgan Housel called “Same as Ever”

Somebody, make me a time machine

Life would be easy if we had a way to accurately predict the consequences of the events/ actions.

Scenario 1 – what would be your reaction if some random person hands you a $1,000,000 lottery ticket and, in few moments, you realize that you just won that lottery?

Scenario 2 – what would happen if an ambitious project that you worked on tirelessly for many years while sacrificing your other priorities – ends into a big failure because of a seemingly impossible and insignificant event/ error?

For most of us these two scenarios are practically impossible but the odds are still non-zero. They can happen in reality.

How can we be sure that they selectively happen to certain person? Scenario 1 for ourselves and Scenario 2 for our enemies especially… (Just kidding)

If you closely observe the lives we are living right now, you will see that we are always oscillating between such events which demand certainty of outcomes even before the are realized. We have this innate urge to remain ready for such events; it is what we are always striving for.

Now, one question – are we living in a matrix? Is universe a simulation?

If the answer is ‘YES’, then it means that every outcome should be predetermined. If everything is predetermined then why things don’t happen the way we ‘want’? Does that mean that we lack the computational capabilities to precisely calculate the outcome? OR is what is destined to happen different from what we ‘want’?

If the answer is ‘NO’, then everything explodes into meaninglessness. The answers are nihilistic.

Looking at the both outcomes of this question we see that we need a baseline to make our decision making effective. Is there a formula to systematically put all the things happening around? What are somethings in nature whose knowledge will ensure our satisfactory existence. (I am being very optimistic while writing ‘satisfactory’ word here.)

In simple words, what is the formula to live a good life? whether it is predictable or not.

 Morgan Housel the famous author of the Psychology of Money wrote one important book called Same as Ever which tries to answer this same question. Same as Ever drives the motto of objective flexibility and subjective awareness of every event happening around us and with us.

This is a deep dive into Morgan Housel’s book “Same as Ever”.

I will try to keep this short. Here are some instructions:

Those who have read this book – each idea in this book is numbered in the sequence Morgan explains in the flow of the book. So, #1 is Hanging by a Thread as mentioned in book and #23 is Wounds heal, Scars last

Those who haven’t read the book – I have given short summary of what Morgan discusses in each of the 23 ideas. That should help you to wrap you head around my distilled down version of this book.

(I apologize for putting that part in the end and spoiling the conclusion/ discussion on this book.)

I would say this book has been one of the most important books I have come across. (I am an average book reader by the way. So, not sure if same would be the case for other people.) While going through each idea, you will realize that something keeps on repeating; and even though it repeats, it brings new perspective into that specific discussion. My attempt to summarize this book focuses on picking what is common but connected to all the facts mentioned in the book and also their connection to the reality we live in.

Discussions

The discussion is in 3 steps, so adjusting our understanding to previous step is key to understand the next step. The illustrative images in each step of the discussion connects the ideas from the book to a common central idea. It will be handy if you read this with the book in your hand or you can jump to the point-to-point summary (the part after conclusion) in a neighboring tab of your web browser.

Step 1 discussion:
Figure 1. Finite and recurring cycle of compounding processes

You will see in the figure 1 that reality is ever changing process of infinite real events. The key to understand what is happening is to see every event containing same potential at first. Keep in mind – same potential – neither good nor bad. Once you assign every event with equal potential you will see that compounding accounts for that single event to build on and create the next event. Sometimes two big events will compound together to create an enormous event.

Now comes the fun part – the enormity of every compounded event will always be in favor of someone and against the favor of the complementary population. This makes that event good or bad for people. Some will suffer some will rejoice.

A person who knows how the world, nature or universe works will not have preferences, favor-ability towards such events. The answer lies in the cyclical nature of such events. Keeping a single event sustained for long duration demands to go many things to work in supporting ways and as every event has same potency in the infinite possibilities, it surely will lead to the downfall of that process. It’s just matter of time.

Talking about matter of time – the game of life is not about winning, rather it is about remaining in the game longer as the compounding pays off and decomposes into new start.

Our limited life span intuitively doesn’t allow us to wait till the compounding pays off. That is exactly where we make mistake. That is exactly why we are devastated by a single seeming insignificant event causing destruction of our favorite things.

Step 2 discussion:
Figure 2. Reality is far from perfect

Our urge to predict everything to ensure survival demands perfection in every entity considered for precision and accuracy of prediction. As reality is made up of many real possibilities, this count of possibilities and the errors associated with their measurements require huge resources which render the prediction process impractical for the possible outcomes.

(Keep in mind right now that we are only talking about those variables, events which we can understand; we haven’t even entered into those variables, events we don’t even understand or know in first place.)

The moment we introduce poorly known, immeasurable but significant variable – the whole game of predictability crumbles down.

That is exactly why instead of striving for better predictability, it is a smart choice to be prepared for everything. Knowing that this too shall end soon should comfort us to prepare for such things/ events. The rejection of the urge for perfection, absoluteness and full efficiency will immediately prepare us for everything that reality unfolds.     

Step 3 discussion:
Figure 3. In the end, we are only human.

Now that we know how every event is potent and can immediately contribute to a cyclical process of compounding, it is important to understand how we comprehend that compounding. As everything that we do is directly linked to our survival we are by default born with preferences. These preferences get eliminated or amplified based on the life experiences we have. Even though our urge for predictability demands objectivity we often forge the subjective parts of every narrative. The subjectivity is important, because the reasons to survive are different for different people.

Conclusion – Human behavior and laws of nature

Our mind rarely understands anything as a flow of entities. Almost all of the fundamental entities existing in nature are flow – continuum entities. But in order to understand them study them we break them into pieces which makes is practical to quantify and predict. For time as an example – we have past – present – future; we need this separation to comprehend the flow of time. This slight arrangement of separation of events just for the convenience of communication and comprehension for our minds has now become such a second nature of our realities that we could hardly come out of the idea of past and future. Past keeps on haunting and future creates anxiety due to the uncertainty. Nostalgia from past brings us joy and what advancements future will present inspires us to work harder today. We rarely notice that this works both ways.

It is really difficult and impractical for our mind to let go of this past-present-future mentality. This convenience of separation for the sake of improving our decision making and survival has imparted a sense of time being a set of discrete isolated events, independent events. This steals the feature of hyper-connectivity in our understanding of reality.

Once we come out of the discretization of time as past-present-future we will see that every event is equally important and highly interconnected and multidimensional (in the sense that it creates multiple real effects on multiple entities) Our mind being biased for survival and in energy optimization mode, it always focuses on what is required to remain alive. This sense of remaining alive now has evolved into intellectual survival – as in what things we define as our life. So, even though from objective point of view all events remain exactly the same, on our personal level certain events are highly important because they change the things we are attached to in a drastic way – in most cases our life. We are now scared to die intellectually – a mental death – the death of our truths – our identity. And trust me, this happens frequently.

Morgan in this book very beautifully noted down the factual version of the reality we live in; it is beautiful because it shows how our human nature is always affecting the seemingly objective reality of the most of the things.

This is my ultimate distilled down version of the book “Same as Ever” by Morgan Housel.  

One point summary of ‘Same as Ever’ by Morgan Housel

 It also highlights that our mind is the first and the easiest one to fool, which leads to false sense of superiority over others and creates biases. Once we accept that nothing is perfect, no one is perfect – it injects humility and forgiveness. It also makes us grateful for what we possess today. What else could be more important than this to be justified as a human being?

These points ask for detachment from predictions and end results. A sense of responsibility for the actions could be the best version of any person – this exactly is invoked when we are trying to prepare for the future instead of striving to predict it.

I think we need more ideas like this when we are fighting for survival for such unimportant things where we already know the real, practical answers but have decided to ignore them.

The ability to see every event at the same level is a superpower any one of us can have.

For those who haven’t read the book here is the point-to-point summary of the book “Same as Ever”:  

#1. If you know where we’ve been you realize, we have no idea where we’re going.

Here, Morgan gives many real-life events where a single decision led to catastrophic events causing loss of many lives and valuable resources.

When we study history even when we know what exactly happened, it is tricky to pinpoint the trigger for that event. There will be why and how behind every small-small event and when we will reach to its origin it becomes really difficult to wrap your mind around that petty thing which had led to such a big and historic event.

The absurdity of past connections should humble your confidence in predicting future ones.

#2. We are very good at predicting the future, except for the surprises – which tend to be all that matter

In very simple words, Morgan highlights the extents of our imagination and thinking. Even though they are infinite, the nature in which we are existing is equally or rather infinite in bigger and greater sense. That is exactly why even when we think we are prepared for everything, nature will always have something new in its pocket to reveal and not being ready for that exact new thing makes that event overwhelming for us because we were not ready for that exact new reveal.

It’s impossible to plan for what you can’t imagine, and the more you think you’ve imagined everything the more shocked you’ll be when something happens that you hadn’t considered.

This itself should humble us. That is why preparation is more important than forecasting.

Invest in preparedness, not in prediction

#3. The first rule of happiness is low expectations.

The most important observation Morgan puts here is in the ways we gauge our resourcefulness – it is always relative – material or immaterial – objects or emotions. We always have a baseline which is created by comparing ourselves with those around us. That is exactly why we rarely appreciate what we have at our hands.

We always crave for what ‘they’ seem to have instead of appreciating what we already and really have in our hands. Even when we are unsure about whether others actually have those things, still we crave those things for us, which is tragic!

Morgan expresses that almost all of the truly precious things in our life don’t come with a price tag that is why we never care to evaluate their importance – like good health, freedom. Same is the case with expectations.

When Morgan is asking for low expectations, it is not omission of the motivation to improve ourselves. Low expectations ask for realistic expectations. One must always be observant of the gap between what we wanted and what happened in reality.

#4. People who think about the world in unique ways you like also think about the world in unique ways you won’t like.

Here, Morgan talks about the role models, heroes, leaders we consider the best of us all. It is very important to understand that they are the best among us all because they did something in very exceptional manner which made them stand out of the well-defined ‘boring’ and ‘average’ structure of the society. If they would have followed the same paths that other followed, they would have been just like others.

In order to stand out of the masses they did something different.

Now be cautious! This different could be seen as good or bad as per the average crowd level. And keep in mind this specialty in that person is because others don’t have it in them. So, in order to create and develop something special out of the same average crowd one has to overcome a resistance of the masses where a trade-off is done with other aspects of their personality. Sometimes the exceptional conditions create exceptional personalities which many people fail to recognize.

Of course they [successful people] have abnormal characteristics. That’s why they’re successful! And there is no world in which we should assume that all those abnormal characteristics are positive, polite, endearing, or appealing.

Simple words, there is always some trade off to achieve something truly exceptional.

You gotta challenge all the assumptions. If you don’t, what is doctrine on day one becomes dogma forever after

#5. People don’t want accuracy. They want certainty.

A common trait of human behavior is the burning desire for certainty despite living in an uncertain and probabilistic world.

Morgan discusses how we are always trying to alleviate the bad results, pain in all life scenarios. The urge to survive supersedes everything. Our brain always wants a confirmed trigger on whether to fight or flight for given problem. It is always in energy optimization mode and in the uncertain world filled of infinite possibilities it wants something to act on immediately. Otherwise, brain knows that it won’t survive. The urge for certainty – that clarity of whether to fight or flight is the most important information than how precisely we are assessing the reality. It’s like brain takes a shortcut to ensure survival. That is exactly why huge load of information especially numbers overwhelm us.

The core is that people think they want an accurate view of the future but what they really crave is certainty.

#6. Stories are always more powerful than statistics.

If we continue the train of thoughts from previous point, soon we will appreciate how dearly we appreciate stories instead of boring numbers. Even when stories would tell a lie and numbers would tell the real, pure truth we would always choose a fake story over realistic numbers. Our brain doesn’t want to overwork itself to ensure survival.

Good stories tend to do that [evoking emotions and connecting the dots in millions of people’s heads]. They have extraordinary ability to inspire and evoke positive emotions, bringing insights and attention to topics that people tend to ignore when they’ve previously been presented with nothing but facts.

Stories create an emotional, empathic bridge between people which our brain already knows since the childhood. The very first think a baby does to start breathing is crying not counting. (I know the analogy is lame but it works here) we are implicitly trained to actively process emotions first and then numbers. Stories enhance this ability on next level.

That is exactly why emotional-ity will always be preferred over rationality.

We live in a world where people are bored, impatient, emotional, and need complicated things distilled into easy-to grasp scenes.

#7. The world is driven by forces that cannot be measured.

Morgan brings here more clarity on the objective nature of the numbers even when they are showing the truth, the reality. The point that our reality is made up of the infinite possibility itself shows that the sheer limitation of our computation capability will create a partial picture of the bigger reality. This happens because many of the factors which influence our reality are beyond quantification.  That is exactly why whenever we are making any decision based on objective and true data (like truest of true numbers) we should bear in mind that these numbers are not accounting for those unmeasured factors which also affect the reality we are trying to understand.

Some things are immeasurably important. They’re either impossible, or too elusive, to quantify. But they can make all the difference in the world, often because their lack of quantification causes people to discount their relevance or even their existence.

In simple words, our story loving brain is driven by intuition and safe/ familiar information which is unquantifiable most of the times.

#8 Crazy doesn’t mean broken. Crazy is normal; beyond the point of crazy is normal.

Morgan is trying to point out how we understand what is means to be at the top. He established that most of the tops we experience in life are to because we have experienced falling down from them and we would have never understood that we were at top unless we have had fall down from them.

The only way to discover the limits of what’s possible is to venture a little way past those limits.

We never appreciate summit of something unless we start climbing from down or fall down from that summit. That is exactly why what made you feel at the top will make you safe and that attachment to safety will lead to your fall, the pain of fall will motivate you to climb new heights and again the cycle will go on.

#9. A good idea on steroids quickly becomes a terrible idea.

Morgan here explains how evolution created the species around us. There was always some trade-off while evolving because of the forces of nature. In nature nothing has absolute competitive advantage otherwise a single species will take over everything that single species alone will lead to its downfall and destruction due to the lack of diversity.

Most things have a natural size and speed and backfire quickly when you push them beyond that.

In simple words, anything that is burns bright, goes out fast. Resources behind every process are limited and even if they would be available in surplus, extent of their utilization affects the outcome and overall integrity of that process.    

#10. Stress focuses your attention in ways that good times can’t.

The urge to survive makes our brain to push to its untested limits. These limits are there just for the optimum behavior so that our brain could actually use the reserve energy when it is the question of life and death. When it come down to do or die – people have always delivered in surprising and shocking ways.

The circumstances that tend to produce the biggest innovations are those that cause people to be worried, scared, and eager to move quickly because their future depends on it.

Morgan points out here that this stress should be healthy because there is always a natural size of everything as explained in point #9.

There is a delicate balance between helpful stress and crippling disaster.

#11. Good news comes from compounding, which always takes time, but bad news comes from a loss in confidence or a catastrophic error that can occur in a blink of an eye.

Growth always fights against competition that slows its rise.

Morgan here shows how things that exist today as our reality have gone through multiple iterations. They have already failed many times and started again long ago; its just that the compounding imparted grandeur and power to fight against the adversities of the life which made their realisation possible here in front of us. There will again be some simple, seemingly insignificant event which will destroy this creation and things will start again.

To enjoy peace, we need almost everyone to make good choices. By contrast, a poor choice by just one side can lead to war.

#12. When little things compound into extraordinary things.

Here Morgan points out from the examples of history how in order to avoid a big calamity people ignored some small incidents which led to even bigger calamities. It is ingrained in our mind to overlook big events because the smaller events which lead to their realization are “small and insignificant”.

Small risks weren’t the alternative to big risks; they were the trigger.

#13. Progress requires optimism and pessimism to coexist.

Morgan here talks about how our preferences for each and everything have stolen away the realism in our lives. Instead of favoring one side, life is more about appreciation of the spectrum. It was never about who wins or who loses because both are short lived. It is always about who survived and stayed in the game longer. (Simon Sinek calls it the infinite game as explained in Game theory.)

The trick in any field – from finance to careers to relationships – is being able to survive the short-run problems so you can stick around long enough to enjoy the long-term growth.

Whoever lives to see the end wins but that victory is just over those who couldn’t survive. There will always be some room at the top because conditions never remain the same.

#14. There is a huge advantage to being a little imperfect.

The more perfect you try to become, the more vulnerable you generally are

The idea of perfection immediately steals the flexibility from any given system. Because of the perfection the system is bound to certain thriving conditions and exactly when you expose this system to the reality of infinite possibilities there will always be some ‘seemingly’ trivial event which will take down that whole system.

A little imperfection makes the system to bend thereby giving place to perform in unimagined conditions and as we have already learnt that the reality is full of unimaginable but real events.

Morgan beautifully explains the ways in which natural evolution has worked out.

A species that evolves to become very good at one thing tends to become vulnerable at another.

…species rarely evolve to become perfect at anything, because perfecting one skill comes at the expense of another skill that will eventually be critical to survival.

Nature’s answer is a lot of good enough, below-potential traits across all species.

#15. Everything worth pursuing comes with a little pain. The trick is not minding that it hurts.

The really important and actually valuable things in life don’t come with a price tag and that is exactly why we are not ready to pay any price. This makes our minds to wish for such things because of the false sense of entitlement. This same entitlement blinds us from the real actions which can lead us to this achievement and we keep on whining about not achieving these things. A wishful thinking!

A unique skill, an underrated skill, is identifying the optimal amount of hassle and nonsense you should put up with to get ahead while getting along.

#16. Most competitive advantages eventually die.

A we have now already understood that even a small event can lead to collapse of any grand creation and how easy it is to undermine any event we must now accept that nothing big will stay as it is now. Same goes for any competitive advantage. As things keep changing the advantages which made their impact big will become irrelevant with the changing things. One has to keep on reinventing in order to remain relevant and effective with the changing times.

Evolution is ruthless and unforgiving – it doesn’t teach by showing you what works but by destroying what doesn’t.

#17. It always feels like we’re falling behind, and it’s easy to discount the potential of new technology.

Morgan highlights how the innovations which we consider ground-breaking, world-changing were result of multiple small-small events creating synergy to coexist.

It’s so easy to underestimate how two small things can compound into an enormous thing.

#18. The grass is greener on the side that’s fertilized with bullshit.

You never know what struggles people are hiding.

As we have already seen our urge to compare our conditions with the conditions of others and always consider ours to be the worst most of the times, it is evident that we are experts in judging everything in its entirety based on very little information. Our biases and basic mentality feed this tendency furthermore. But reality is always like the iceberg.

Most of the things are harder than they look and not as fun as they seem.

#19. When the incentives are crazy, the behavior is crazy. People can be led to justify and defend nearly anything.

Morgan here shows that beyond envy people are driven by incentives. You can make people do almost anything, make them believe them in almost any thing if their interests are aligned in that. This is strong when people are helpless and when it is about their survival.

One of the strongest pulls of incentives is the desire for the people to hear only what they want to hear and see only what they want to see.

The beauty that Morgan points out is that this can also be used to bring good out of people.

It’s easy to underestimate how much good people can do, how talented they can become, and what they can accomplish when they operate in a world where their incentives are aligned towards progress.

#20. Nothing is more persuasive than what you’ve experienced first-hand.

As we have emotional beings and we have already seen that we will always prefer emotional clarity of falsehood over the numerical, arithmetic truth it shows that every part of our understanding of life is tied to our own individual experiences. We rarely appreciate the foretold truth. But we will appreciate all those things which we experience on our own.

That is also why there are certain truths which very few people have experienced but are not generally accepted by the masses because there is no part to connect personally. We can only connect personally only when we have passed through those experiences.

That is exactly why it is difficult to convince people of something really exceptional and extraordinary personal experience, that also why it is also easy to fool people.

The next generation never learns anything from the previous one until it’s brought home with a hammer… I’ve wondered why the nest generation can’t profit from the generation before, but they never do until they get knocked in the head by experience.

#21. Saying “I’m in it for the long run” is a bit like standing at the base of Mount Everest, pointing to the top, and saying, “That’s where I’m heading.” Well, that’s nice. Now comes the test.

In simple words, Morgan shows us that we rarely will ever know what we have signed up for. Most of the times our simulative experiences and thoughts will be broken down by the unimaginable possibilities of the reality. Instead of craving for that summit one must try to stand strong while they have started this journey and remain faithful to this step they are taking ahead. This attitude has to be kept with every step which very few people maintain.

Long term is less about time horizon and more about flexibility.

#22. There are no points awarded for difficulty.

Almost all of the times people appreciate certain things, certain people because they couldn’t not have or become like them. This crates a mysticism. We are always attracted to mystical things because the urge to know better (to improve chances of survival against unknown) is our hidden trait.

Complexity creates this mysticism instantly. That is why we most of the time reject truths which are so obvious and in front of our eyes and accept that intellectually stimulating complicated lie. The complexity makes our brain to actively engage in that thing which creates an attachment just because our brain was invested in it.

Complexity gives a comforting impression of control while simplicity is hard to distinguish from cluelessness.

#23. What have you experienced that I haven’t that makes you believe what you do? And would I think about the world like you do if I experienced what you have?

Morgan points out that our lives even though we have common experiences, we associate ourselves to certain groups, certain ideologies on deeper levels and at core we are totally different and individual.

Many debates are not actual disagreements; they’re people with different experiences talking over each other.

References:

  1. Morgan Housel’s book “Same a s Ever”.
  2. Morgan Housel

Logarithmic Harmony in Natural Chaos

Mathematics is one powerful tool to make sense out of randomness but bear in mind that not every randomness could be handled effectively with the mathematical tools we have at our disposal today. One of such tools called Benford’s Law proves that nature works in logarithmic growth and not in linear growth. The Benford’s law helps us to make sense of the natural randomness generated around us all the time. This is also one of the first-hand tools used by forensic accountants to detect possible financial frauds. It is one phenomenal part of mathematics which finds patterns in sheer chaos of the randomness of our existence.

Benford’s Law for natural datasets and financial fraud detection

People can find patterns in all kinds of random events. It is called apophenia. It is the tendency we humans have to find meaning in disconnected information.

Dan Chaon, American Novelist

Is There Any Meaning in Randomness?

We all understand that life without numbers is meaningless. Every single moment gazillions and gazillions of numbers are getting generated. Even when I am typing this and when you are reading this – some mathematical processing is happening in bits of the computer to make it happen. If we try to grasp/understand the quantity of numbers that are getting generated continuously, even the lifetime equivalent to the age of our Universe (13.7 billion) will fall short.

Mathematics can be attributed to an art of finding patterns based on certain set of reasoning. You have certain observations which are always true and you use these truths to establish the bigger truths. Psychologically we humans are tuned to pattern recognition, patterns bring in that predictability, predictability brings in safety because one has knowledge of future to certain extent which guarantees the higher chances of survival. So, larger understanding of mathematics in a way ensures better chances of survival per say. This is oversimplification, but you get the point.

Right from understanding the patterns in the cycles of days and nights, summers, and winters till the patterns in movements of the celestial bodies, the vibration of atoms, we have had many breakthroughs in the “pattern recognition”. If one is successful enough to develop a structured and objective reasoning behind such patterns, then predicting the fate of any process happening (and would be happening) which follows that pattern is a piece of cake. Thus, the power to see the patterns in the randomness is kind of a superpower that we humans possess. It’s like a crude version of mini-time machine.

Randomness inherently means that it is difficult to make any sense of the given condition, we cannot predict it effectively. Mathematics is one powerful tool to make sense out of randomness but bear in mind that not every randomness could be handled effectively with the mathematical tools we have at our disposal today. Mathematics is still evolving and will continue to evolve and there is not end to this evolution – we will never know everything that is there to know. (it’s not a feeling rather it is proved by Gödel’s incompleteness theorem.)

You must also appreciate that to see the patterns in any given randomness, one needs to create a totally different perspective. Once this perspective is developed then it no longer remains random. So, every randomness is random until we don’t have a different perspective about it.

So, is there any way to have a perspective on the gazillions of the numbers getting generated around us during transactions, interactions, transformations?

The answer is Yes! Definitely, there is a pattern in this randomness!!

Today we will be seeing that pattern in detail.

Natural Series – Real Life Data       

Take your account statement for an example. You will see all your transactions, debit amount, credit amount, current balance in the account. There is no way to make sense out of how the numbers that are generated, the only logic behind those numbers in account statement is that you paid someone certain amount and someone paid you certain amount. It is just net balance of those transactions. You had certain urgency someday that is why you spent certain amount on that day, you once had craving for that cake hence you bought that cake, you were rooting for that concert ticket hence you paid for that ticket, on one bad day you faced certain emergency and had to pay the bills to sort things out. Similarly, you did your job/ work hence you got compensated for those tasks – someone paid you for that, you saved some funds in deposits and hence that interest was paid to you, you sold some stocks hence that value was paid to you.

The reason to explain this example to such details is to clarify that even though you have control over your funds, you actually cannot control every penny in your account to that exact number that you desire. This is an example of natural data series. Even though you have full control over your transactions, how you account will turn out is driven by certain fundamental rules of debit/ credit and interest. The interactions of these accounting phenomenon are so intertwined that ultimately it becomes difficult to predict down to every last penny.

Rainfall all around the Earth is very difficult to predict to its highest precision due to many intermingling and unpredictable events in nature. So, by default finding trend in the average rainfall happened in given set of places is difficult. But we deep down know that if we know certain things about rainfall in given regions we can make better predictions about other regions in a better way, because there are certain fundamental predictable laws which govern the rainfall.  

The GDP of the nations (if reported transparently) is also very difficult to pin down to exact number, we always have an estimate, because there are many factors which affect that final number, same goes for the population, we can only predict how it would grow but it is difficult to pin point the number.

These are all examples of real life data points which are generated randomly during natural activities, natural transactions. We know the reason for these numbers but as the factors involved are so many it is very difficult to find the pattern in this randomness.

I Lied – There is A Pattern in The Natural Randomness!

What if I told you that there is certain trend and reference to the randomness of the numbers generated “naturally”? Be cautious – I am not saying that I can predict the market trend of certain stocks; I am saying that the numbers generated in any natural processes have preference – the pattern is not predictive rather it only reveals when you have certain bunch of data already at hand – it is retrospective.

Even though it is retrospective, it can help us to identify what was manipulated, whether someone tried to tamper with the natural flow of the process, whether there was a mechanical/ instrument bias in data generation, whether there was any human bias in the data generation?

Logarithm and Newcomb

Simon Newcomb (1835-1909) a Canadian-American astronomer once realized that his colleagues are using the initial pages of log table more than the other pages. The starting pages of log tables were more soiled, used than the later pages.

Simon Newcomb

Log tables were instrumental in number crunching before the invention of any type of calculators. The log tables start with 10 and end in 99.

Newcomb felt that the people using log tables for their calculations have more 1’s in their datasets repetitively in early digits that is why the initial pages where the numbers start with 1 are used more. He also knew that the numbers used in such astronomical calculations are the numbers available naturally. These numbers are not generated out randomly, they signify certain quantities attributed to the things available in nature (like diameter of a planet, distance between stars, intensity of light, radius of curvature of certain planet’s orbit). These were not some “cooked up” numbers, even though they were random but they had natural reason to exist in a way.

He published an article about this but it went unnoticed as there was no way to justify this in a mathematical way. His publication lacked that mathematical rigor to justify his intuition.

Newcomb wrote:

“That the ten digits do not occur with equal frequency must be evident to anyone making much use of logarithmic tables, and noticing how much faster the first one wears out than the last ones.”   

On superficial inquiry, anyone would feel that this observation is biased. It seemed counterintuitive, also Newcomb just reported the observation and did not explain in detail why it would happen. So, this observation went underground with the flow of time.

Frank Benford and The Law of Anomalous Numbers

Question – for a big enough dataset, how frequently any number would appear in first place? What is the probability of numbers from 1 to 9 to be the leading digit in given dataset?

Intuitively, one would think that any number can happen to be in the leading place for given dataset. If the dataset becomes large enough, all nine numbers will have equal chance to be in first place.

Frank Benford during his tenure in General Electric as a physicist made same observation about the log table as did Newcomb before him. But this time Frank traced back the experiments and hence the datasets from these experiments for which the log table was used and also some other data sets from magazines. He compiled some 20,000 data points from completely unrelated experiments and found one unique pattern!

Frank Benford

He realized that even though our intuition says that any number from 1 to 9 could appear as the leading digit with equal chance, “natural data” does not accept that equal chance. The term “Natural data” refers to the data representing any quantifiable attribution of real phenomenon, object around us, it is not a random number created purposefully or mechanically; it has some origin in nature however random it may seem.

Frank Benford thus discovered an anomaly in natural datasets that their leading digit is more 1 or two than the remaining ones (3,4,5,6,7,8,9). In simple words, you will see 1 as leading digit more often in the natural datasets than the rest of the numbers. As we go on with other numbers the chances that other numbers will be frequent in leading position are very less.

In simple words, any naturally occurring entity will have more frequent 1’s in its leading digits that the rest numbers.

Here is the sample of the datasets Frank Benford used to find this pattern:

Dataset used by Frank Benford in his 1938 paper “The Law of Anomalous Numbers”

So, according to Benford’s observations for any given “natural dataset” the chance of 1 being the leading digit (the first digit of the number) is almost 30%. 30% of the digits in given natural dataset will start with 1 and as we go on the chances of other numbers to appear frequent drop drastically. Meaning that very few number in given natural data set will start with 7,8,9.

Thus, the statement of Benford’s law is given as:

The frequency of the first digit in a populations’ numbers decreases with the increasing value of the number in the first digit.

Simply explained, as we go on from 1 to 9 as first digit in given dataset, the possibility of their reappearance goes on reducing.

1 will be the most repeated as the first number then 2 will be frequent but not more than 1 and the frequency of reappearance will reduce and flatten out till 9. 9 will rarely be seen as the leading digit.

The reason why this behavior is called as Benford’s Law (and not Newcomb’s Law) is due to the mathematical equation that Benford established.

Where, P(d) is the probability that a number starts with digit d. Digit d could be anything 1,2,3,4,5,6,8 or 9.

If we see the real-life examples, you will instantly realize how counterintuitive this law is and still nature chooses to follow it.

Here are some examples:

I have also attached an excel sheet for complete datasets and to demonstrate how simply one can calculate and verify Benford’s law.

Population of countries in the world –

The dataset contains population of 234 regions in the world. And you will see that 1 appears the most as first digit in this dataset. Most of the population numbers start with 1 (70 times out of 234) and rarely with 9 (9 times out of 234)

Country-wise average precipitation –

The dataset contains average rainfall from 146 countries in the world. Again, same pattern emerges.

Country wise Gross Domestic Product –

The dataset contains 177 countries’ GDP in USD. See the probability yourself:

Country-wise CO2 emissions:

The data contains 177 entries

Country wise Covid cases:

Here is one more interesting example:

The quarterly revenue of Microsoft since its listing also shows pattern of Benford’s Law!

To generalize we can find the trend of all these data points by averaging as follows:

This is exactly how Benford avearaged his data points to establish a generalized equation.

Theoretical Benford fit is calculated using the Benford equation expressed earlier.

So here is the relationship graphically:

Now, you will appreciate the beauty of Benford’s law and despite seeming counterintuitive, it proves how seemingly random natural dataset has preferences.

Benford’s Law in Fraud Detection

In his 1938 paper “The Law of Anomalous Numbers” Frank Benford beautifully showed the pattern that natural datasets prefer but he did not identify any uses of this phenomena.

1970 – Hal Varian, a Professor in University of California Berkely School of Information explained that this law could be used to detect possible fraud in any presented socioeconomic information.

Hal Varian

1988 – Ted Hill, an American mathematician found out that people cannot cook up some numbers and still stick to the Benford’s Law.

Ted Hill

When people try to cook up some numbers in big data sets, they reflect certain biases to certain numbers, however random number they may put in the entries there is a reflection of their preference to certain numbers. Forensic accountants are well aware of this fact.    

The scene where Christian pinpoints the finance fraud [Warner Bros. – The Accountant (2016)]

1992 – Mark Nigrini, a South African chartered accountant published how Benford’s law could be used for fraud detection in his thesis.

Mark Nigrini

Benford’s Law is allowed as a proof to demonstrate accounts fraud in US courts at all levels and is also used internationally to prove finance frauds.

It is very important to point the human factor, psychological factor of a person who is committing such numbers fraud. People do not naturally assume that some digits occur more frequently while cooking up numbers. Even when we would start generating random numbers in our mind, our subconscious preference to certain numbers gives a pattern. Larger the data size more it will lean to Benford’s behavior and easier will be the fraud detection.

Now, I pose one question here!

If the fraudster understands that there is such thing like Benford’s Law, then wouldn’t he cook up numbers which seem to follow the Benford’s Law? (Don’t doubt my intentions, I am just like a cop thinking like thieves to anticipate their next move!!!)

So, the answer to this doubt is hopeful!

The data generated in account statements is so huge and has multiple magnitudes that it is very difficult for a human mind to cook up numbers artificially and evade from detection.

Also, forensic accountants have showed that Benford’s Law is a partially negative rule; this means that if the law is not followed then it is possible that the dataset was tampered/ manipulated but conversely if the data set fits exactly / snuggly with the Benford’s law then also there is a chance that the data was tampered. Someone made sure that the cooked-up data would fit the Benford’s Law to avoid doubts!

Limitations of Benford’s Law

You must appreciate that nature has its ways to prefer certain digits in its creations. Random numbers generated by computer do not follow Benford’s Law thereby showing their artificiality.

Wherever there is natural dataset, the Benford’ Law will hold true.

1961 – Roger Pinkham established one important observation for any natural dataset thereby Benford’s Law. Pinkham said that for any law to demonstrate the behavior of natural dataset, it must be independent of scale. Meaning that any law showing nature’s pattern must be scale invariant.

In really simple words, if I change the units of given natural dataset, the Benford law will still hold true. If given account transactions in US Dollars for which Benford’s Law is holding true, the same money expressed in Indian Rupees will still abide to the Benford’s Law. Converting Dollars to Rupees is scaling the dataset. That is exactly why Benford’s Law is really robust!

After understanding all these features of Benford’s Law, one must think it like a weapon which holds enormous power! So, let us have some clarity on where it fails.

  1. Benford’s Law is reflected in large datasets. Few entries in a data series will rarely show Benford’s Law. Not just large dataset but the bigger order of magnitude must also be there to be able to apply Benford’s Law effectively.
  2. The data must describe same object. Meaning that the dataset should be of one feature like debit only dataset, credit only dataset, number of unemployed people per 1000 people in population. Mixture of datapoints will not reflect fit to Benford’s Law.
  3. There should not be inherently defined upper and lower bound to the dataset. For example, 1 million datapoints of height of people will not follow Benford’s Law, because human heights do not vary drastically, very few people are exceptionally tall or short. This, also means that any dataset which follows Normal Distribution (Bell Curve behavior) will not follow Benford’s Law.
  4. The numbers should not be defined with certain conscious rules like mobile numbers which compulsorily start with 7,8, or 9; like number plates restricted 4, 8,12 digits only.
  5. Benford’s Law will never pinpoint where exactly fraud has happened. There will always be need for in depth investigation to locate the event and location of the fraud. Benford’s Law only ensures that the big picture is holding true.

Hence, the examples I presented earlier to show the beauty of Benford’s Law are purposefully selected to not have these limitations. These datasets have not bounds, the order of magnitude of data is big, range is really wide compared to the number of observations.     

Now, if I try to implement the Benford’s Law to the yearly revenue of Microsoft it reflects something like this:

Don’t freak out as the data does not fully stick to the Benford’s Law, rather notice that for the same time window if my number of datapoints are reduced, the dataset tends to deviate from Benford’ Law theoretically. Please also note that 1 is still appearing as the leading digit very frequently, so good news for MICROSOFT stock holders!!!

In same way, if you see the data points for global average temperatures (in Kelvin) country-wise it will not fit the Benford’s Law; because there is no drastic variation in average temperatures in any given region.

See there are 205 datapoints – big enough, but the temperatures are bound to a narrow range. Order of magnitude is small. Notice that it doesn’t matter if I express temperature in degree Celsius of in Kelvins as Benford’s Law is independent of scale.

Nature Builds Through Compounded Growth, Not Through Linear Growth!

Once you get the hold of Benford’s law, you will appreciate how nature decides its ways of working and creating. The Logarithmic law given by Frank Benford is a special case of compounded growth (formula of compound interest). Even though we are taught growth of numbers in a periodic and linear ways we are masked from the logarithmic nature of the reality. Frank Benford in the conclusion of his 1937 paper mentions that our perception of light, sound is always in logarithmic scale. (any sound engineer or any lighting engineer know this by default) The growth of human population, growth of bacteria, spread of Covid follow this exponential growth. The Fibonacci sequence is an exponential growth series which is observed to be at the heart of nature’s creation. That is why any artificial data set won’t fully stick to logarithmic growth behavior. (You can use this against machine warfare in future!) This also strengthens the belief that nature thinks in mathematics. Despite seemingly random chaos, it holds certain predictive pattern in its heart. Benford’s Law thus is an epitome of nature’s artistic ability to hold harmony in chaos!  

You can download this excel file to understand how Benford’s law can be validated in simple excel sheet:


benford-partsperbillionDownload

References and further reading:

  1. Cover image – Wassily Kandinsky’s Yellow Point 1924
  2. The Law of Anomalous Numbers, Frank Benford, (1938), Proceedings of the American Philosophical Society
  3. On the Distribution of First Significant Digits, RS Pinkham (1961), The Annals of Mathematical Statistics
  4. What Is Benford’s Law? Why This Unexpected Pattern of Numbers Is Everywhere, Jack Murtagh, Scientific American
  5. Using Excel and Benford’s Law to detect fraud, J. Carlton Collins, CPA, Journal of Accountancy
  6. Benford’s Law, Adrian Jamain, DJ Hand, Maryse Bйeguin, (2001), Imperial College London
  7. data source – Microsoft revenue – stockanalysis.com
  8. data source – Population – worldometers.info
  9. data source – Covid cases – tradingeconomics.com
  10. data source – GDP- worldometers.info
  11. data source – CO2 emissions – worldometers.info
  12. data source – unemployment – tradingeconomics.com
  13. data source – temperature – tradingeconomics.com
  14. data source – precipitation – tradingeconomics.com

Entrepreneurship and Poverty

We are surrounded by many entrepreneurs which go unnoticed and have nothing to do with the keywords like technology, unicorn, angel investors. A high chunk of these unnoticed entrepreneurs are poor entrepreneurs, almost a billion around the world. Nobel laureate economists Abhijit Banerjee and Esther Duflo studied such poor entrepreneurs which has created deep insights and answered many questions. Providing supporting capital – microcredit to such poor entrepreneurs is not the final answer to this riddle.

Paying close attention to the larger fraction of the poor entrepreneurs

Monthly Revenue of a ‘Chai-wala’

It is very common discussion among group of youngsters to roughly estimate revenue of their “Snacks n’ Tea” seller while enjoying that short break. The discussion ends when the earnings estimate from that seller’s business reaches to a figure which is far bigger than what these “highly qualified” youngsters actually earn thereby inspiring them to think about pursuing their own business, start-up. What actually happens after such short surge of inspiration is also a common knowledge. Very few of such people actually work on entrepreneurship, their business idea and again very few of these truly taste the success. Social media, mainstream media have also positively affected and boosted the startup mentality, entrepreneur mentality among the youngsters through TV-series, reality shows, success stories, popular talk shows, podcasts and nonetheless video platforms like YouTube. The “F.I.R.E. culture” (Financially independent, Retire early) is also one wave of thought which inspires such entrepreneurs to create something of value, turn it into a business and sell it at higher valuation to gain financial independence early in life. (Although, FIRE is not limited to financial freedom through entrepreneurship only). Following their passion and working over it to create a start-up and then becoming a wealthy person is also one famous new career route for today’s youngsters.

In short, for our generation, entrepreneurship holds the key to financial independence thereby key to the freedom (materialistic freedom to be more specific) – life living on their own terms, without any terms and conditions.

When looked through “the pop-cultural” lens towards entrepreneurship one will see all the glamour, money, popularity, angel investors, “unicorn startup” funds and success stories. In reality there are very few practical examples in these enterprises which successfully fit to all such criterion, which really have created value in the society; most of them are actually just publicized bubbles rather black holes sucking in the attention, time and money of the investors.

The Reality of Entrepreneurship Around the World

Start-ups represent only the early developmental part of an entrepreneurship. Even though they represent such an early and small part of the concept of entrepreneurship, start-up stands as the biggest lamp, biggest fire attracting the youth like moths.

Here are some interesting facts:

9 out of 10 startups fail

7.5 out of 10 venture-backed startups fail

2 out of 10 new businesses fail in the first year of operations

Only 1% of startups become unicorn firms like Uber, Airbnb, Slack, Stripe, and Docker

The success percentage for first-time founders is 18%

20% start-ups fail before the end of their 1st year, and almost 70% start-ups end by their 10th year.

These facts are not presented to demean the value of stat-ups or to negatively criticize start-ups thereby idea of entrepreneurship (although there are some people who also try to capitalize their failure in both the good and bad ways). When you will look at the complementary positive data on start-ups you will realize that the successful start-ups even being low in numbers created value to the society in totally different ways, they changed the ways of working and doing things through the exploitation of technology.

The glamour while portraying the concept of entrepreneurship is actually overshadowing the key idea behind it which is “ingenuity”.

Poor Entrepreneurs

What is the definition of an entrepreneur? The dictionary definition goes like this- “a person who sets up a business or businesses, taking on financial risks in the hope of profit.” Literally, a person who runs an enterprise. Now look at the pictures above, can you tell which one of these is an entrepreneur?

This will make us realize that how the glamour built around the word entrepreneur is actually a mirage. The basic idea in entrepreneurship is the risk taking for the gaining profit. We are surrounded by such small entrepreneurs in our day-to-day life, most of these are poor entrepreneurs. World renowned Nobel laureate economists Abhijit Banerjee and Esther Duflo have contributed to uncover the reality of such poor entrepreneurs and many questions associated with such poverty.

Why should one be interested in poor entrepreneurs?

According to the data collected by Abhijit Banerjee and his team roughly 12% of the population in rich countries calls themselves as self-employed i.e., entrepreneurs. The interesting thing is that the poor countries have far higher percentage of self-employed people. Nearly 70% people call themselves entrepreneurs – self-employed in poor countries. These are the people who are mostly single person entrepreneurs like tailors, bricklayers, auto-drivers, street-vendors, shopkeepers.

“…most income groups in poor countries seem to be more entrepreneurial than their counterparts in the developed world-the poor no less so than others… ”

Abhijit Banerjee and Esther Duflo, Poor Economics – rethinking poverty and the ways to end it

Looks like bigger chunk of the entrepreneurial population of the world is not really glamorous and full of revenues, capital and resources. The intention to focus on this information is not to degrade entrepreneurship, rather it is to understand why the percentage of entrepreneurship is huge in poor countries where availability of resources and capital is already hitting rock bottom low? How do they manage such ventures in low margins? Do these entrepreneurial ventures bring them out of the poverty? If yes then, how? If not then why?

If entrepreneurship is supposed to give people freedom to operate on their own conditions, freedom to be their own boss, freedom to take control over their own lives, bring their ideas into the society then why poor countries where the entrepreneurial fraction is huge are not coming out of poverty? Why most of such poor entrepreneurs remain poor even after embarking on the journey of self-employment?

Trust me the answer is not related to ‘lower rates of returns’ only!

Ingenuity of the Poor Entrepreneurs

Let us understand the challenges faced by the poor entrepreneurs listed as below:

  1. Being poor, they are inherently low on capital (obviously)
  2. They have low or no access to formal financing institutions like banks, insurance companies
  3. As they have no access to formal finance, they approach local moneylenders and borrow with high rates of interest
  4. They have very low risk-taking capacity because any investment other than that for sustenance is a survival challenge
  5. They have very crude social support in terms of materialistic and emotional levels. They are surrounded by people having same difficult lives. They rarely have good connections with people who will trust them, people who will have access to better conditions capital-wise or relation-wise   

Even after having these challenges, the fraction of entrepreneurs in poor countries is surprisingly high. How is this possible?

As Abhijit Banerjee explains, the poor entrepreneurs have clever ideas to run their businesses even at low capital. The unavailability of resources, material/ capital means forces them to find out new creative ways to make living. You will see many such innovative entrepreneurs around who try to make living by using some really interesting ideas e.g., the human hair collectors roaming around town to exchange with utensils/toys, the scrap collectors who collect specific types of waste only and sell them to bigger scrap dealers in bulk, there are some dust collectors in the gold markets of many cities in India where poor people collect road dust around the gold shops and try to extract tiny amount of gold from such collected dust to sell it.

But how many of these innovative, creative and ventures with true ingenuity actually turn into a unicorn or a big company? In simple words, one knows how costly are the hair extensions/ wigs are then why the hair collectors are not getting rich with their business? If gold is that precious then why these dust collectors are not getting rich with this gold dust collection ventures?

This is where the insights created by Abhijit Banerjee play a very vital role. In his book “Poor Economics – rethinking poverty and ways to end it” co-authored by Esther Duflo, he has given very important insights into the world of poor people, the challenges they face and ways to uplift them.

Let us deep dive into the key concepts to understand the economics of such entrepreneurs.

Representation of the Poverty

Figure 1 The S-shaped curve and the poverty trap
Source: Poor Economics – rethinking poverty and the ways to end it by Abhijit Banerjee and Esther Duflo

Economists use the diagram shown above to indicate the relation between income of today and the income a person will earn in the future. You will see an S -shaped curve forming. The red zone indicates the poverty trap zone where a poor person starts from A1 earns a meager amount which is not enough to sustain making the net income negative thereby proceeding to A2 which is backward directed/ decline in income. This reduced income restricts his/her freedom to choose (as the words go “beggars cannot be choosers”), risk-taking ability, reduction in available capital thereby scarcity of capital disposable to meet the daily basic requirements. So, the ventures in which poor people are engaged are down-valuing ventures according to this representation – which is used to represent “The Poverty Trap”. For those who think that the ventures of poor people always end up in losses thereby degrading their existing states, this curve in red zone represents that vicious cycle.

Most of the economists think that poverty is not a vicious cycle. By providing minimum enough capital/ resources to the lowermost group, their lives can be kick-started where the ventures will give net positive incomes, thereby gradually increasing their income over the time. That is why the world around us is explained by blue shaded part of the diagram, known as inverted L-shaped curve.

Figure 2 The inverted L-shaped curve
Source: Poor Economics – rethinking poverty and the ways to end it by Abhijit Banerjee and Esther Duflo

Please note one interesting detail in this diagram which we will bring further in our discussion. The initial slope of the curve is steep indicating substantial valuation increase in income but as the curve proceeds slope of the curve ends into flat thereby indicating less or no increase in valuation of the income over the longer period.

 In very simple words, a venture can only sustain over the time if there is some net gain over the time (always remaining net positive, even if it becomes smaller and stagnant over time). Very few people and actually no one would engage in a venture where they see their future valuation, future earnings dropping over the long-time horizon. That why most of the economist accept Figure 2 to represent the incomes of today and tomorrow for anyone.

Asking the Right Questions

Now that we have realized that it will take very small amount of effort and capital to uplift the poor entrepreneurs why doesn’t that help them immediately? Abhijit Banerjee in his studies asked some important questions which reveal why just giving poor enough money won’t solve the complete problem. Abhijit Banerjee clarifies that it is the inherent nature of the enterprises/ businesses, societal conditions and even the mindset of the poor entrepreneurs that makes them stagnant in their ventures. Even if they are running their small businesses successfully, they will always make just enough to sustain in long time horizon, very few will be the outliers which come out of this stagnancy.

Abhijit Banerjee pointed out that most of the poor entrepreneurs repay their loans on high interest rates. The high returns rates are attributed to the lending from informal financiers like local money lenders, relatives. If poor entrepreneurs are successfully repaying such high interest loans while sustaining through the business, then that means that their overall rate/ fraction of earning for the capital invested is also very high.

So, why don’t they become relatively wealthy even after running business with high rate of overall returns?  

Here we can take support of the inverted L-shaped curve for poor entrepreneurs and build on that further.

Figure 3 Diminishing marginal returns in poor enterprises
Figure created from the explanation in the book Poor Economics – rethinking poverty and the ways to end it by Abhijit Banerjee and Esther Duflo

Abhijit Banerjee explained the reasons for the stagnancy in poor enterprises in practical ways based on his field research. He explains the important behavior of marginal returns in terms of the poor enterprises. Marginal returns are the what left after an entrepreneur pays off everything – like payment on tools, payment of the wages to the workers, payment of the things bought to sell. Marginal return is take-home money after the business is done.

Now let us see the inverted L-shaped curve in figure 3 for poor enterprises. At the start of the business the marginal returns (shown as the height of the vertical blue arrow) are very high for the extra capital invested (shown as the length of the black horizontal arrow). The early investments in the business yields higher returns – higher marginal returns.

But, as the curve proceeds, due to the inherent nature of the businesses poor entrepreneurs are involved in as the capital investment goes on increasing, for every unit increase in such investment the marginal returns go on reducing and diminish further.

You can see in the figure 3, there are four different instances of extra capital investment in the poor enterprises. The L-shaped curve increases rapidly at early investment stage but as the capital investment goes on increasing the curve quickly flattens out, indicating the stagnancy.

In poor enterprises any new unit capital investment will give diminished marginal returns over the time

This behavior can be explained by the example of local fruits and vegetable vendors. First a person starts out with very few 2 or 3 vegetables (potato, tomato, onions for example). Being the commodity vegetables, they are sold very easily, fast and margins are also pretty good for the amount invested to buy them in wholesale. So, with those good returns he/she now buys different vegetables and now provide more options to his/ her customers. Now you will realize that not everyone buys every vegetable he/she has to offer, the sell of potato, tomato, onions may still remain good. But in order to expand he/she cannot depend on selling those only, and as he/ she expands into new varieties there comes the uncertainty of not everyone buying it. Perishable nature of these products is also one problem over which he/she has no control. The overall return may increase by incorporating more variety of items or by buying a cart to access many customers but for every new investment further done to grow this business, the guarantee of higher returns is very low.

So, the vegetable/ fruit vendor realizes this at a stage in his/her business that buying only those items which would sell, items which will not perish immediately with limited customer accessibility through cart is the only option to survive. You have to understand the limitations created by the nature of the businesses poor entrepreneurs are invested in.

That is exactly why only giving money to poor entrepreneurs won’t bring them out of the poverty. The businesses they can perform stagnate very rapidly.

Now, someone should ask the question for the case of the vegetable/ fruit vendor.

The questions could be asked as follows,

  1. The vendor should buy a vehicle so that he will contact more customers, why doesn’t he / she do so?
  2. The vendor should go to the wholesale market to buy the vegetables and fruits even at low rates to increase his margins, what stops him/ her?
  3. The vendor should rent a place in cold storage to maintain his items fresh till they are sold to the end customer, what is the hurdle?

Now, let us assume ourselves as this vendor and try to answer these questions.

  1. If the sell is stagnant even with a cart, why should one put exceedingly high amount in a vehicle purchase. This will be a big capital step. As the accessibility to formal lending is difficult, it brings capital in but the returns will be very low due to the borrowing at higher rates of interest.
  2. In order to buy at wholesale low rates connections with the wholesale tycoons are vital. Such connections are based on mutual benefits which the poor entrepreneurs hardly have access to.
  3. Cold storage rentals are significantly high for the amounts they earn so that goes there.

You must understand that these are not some contrived examples created to prove certain points. These are real life challenges and questions faced by poor entrepreneurs. It is only because of such challenges the poor entrepreneurs have that creative mindset, low cost, less capital-intensive problem-solving mindset. This also the reason economists found that poor entrepreneurs have very low number of people involved per business, they cannot afford to employ others due to the stagnancy.

As the study done by Abhijit Banerjee indicates, even if you provide some extra marginal income to the poor entrepreneurs so that they can access such options where extra capital is required, they will still choose to not invest that extra amount in the business because they know that for that extra investment the returns will not be that high over the longer period. (Abhijit Banerjee experimented with such extra capital provisions to poor entrepreneurs in Sri Lanka through lottery system, these entrepreneurs chose to invest that extra money in their livelihoods instead of businesses)  

The Big Gap to Fill

Now you should understand that even when extra capital is provided, that extra capital definitely won’t go into the growth of the poor enterprises. The question now comes that why poor entrepreneurs don’t have wide mindset? Why can’t they think big? Looks like the horizons and the mindset of poor entrepreneurs are so narrow that they are scared of risk taking. For the exact reasons the micro-financing institutions have tried to disseminate finance education, entrepreneurial education to the poor entrepreneur they lent money. But economists found that it is the inherent nature of the enterprises that poor can and are involved in, which makes them to think so.

Abhijit Banerjee here clarifies what exactly is the difference between the poor entrepreneurs and the rich entrepreneurs. For that let us look at the figure 4

Figure 4 Combining technologies and S-shaped curve of entrepreneurship
Source: Poor Economics – rethinking poverty and the ways to end it by Abhijit Banerjee and Esther Duflo

You must appreciate the beauty with which Abhijit Banerjee has explained the difference between poor and rich entrepreneurs. Any incorporation of production technology in an enterprise will improve the productivity. Buying machinery, tools, infrastructures can largely boost the business performance. This boost due to production technology is shown as curve QR.

What does the curve OP represent?

As you have already seen, curve OP starts with no to less capital investment and flatten out immediately. It is the curve of poor entrepreneurship.

Now you must understand that in order to gain marginally/ exceptionally high returns one needs to start with high up-front capital in hand (Indicated as capital OQ). The big tech startups, the big supermarket chains start exactly from here where there are high chances of success (This is also why rich start-ups or any non-poor start-ups demand high funding).

In the case of high marginal returns in poor enterprises in their early stages of development we can easily think that high marginal returns should create the foundation of a successful long-term business. These high margins will allow the person to invest more in the same business, to employ more people to expand the workforce, to purchase new machinery, new tools. But these high marginal returns could never fill that capital gap for poor. This is what majorly differentiates between poor and rich entrepreneurs.

So, one has to really appreciate the gap lying between poor and rich entrepreneurs. This gap of capital to create production technology is too large for poor entrepreneurs and for the business they run. It is not just their narrow mindset, rather they are so close to the harsh reality that they prefer not to follow such seemingly “imaginary” paths.

Conclusion

Entrepreneurship for our young generation seems like a glamorous venture with big money, new technologies, new ideas, new technologies, “angel” investors and “unicorn” start-ups but we always forget that we are surrounded by many entrepreneurs which go unnoticed and have less to nothing to do with the keywords explained here.

A high chunk of these unnoticed entrepreneurs are poor entrepreneurs. They are part of our lives in a big way – you can think of the vendors of every small thing you use in your whole day.

Most of the people in poor countries are self-employed or entrepreneurs. This proportion is far less in developed nations.

Poor entrepreneurs seem to make high returns in their business but most of those high returns go to the repayment of the loans at high interest rates due to the inaccessibility to formal financial institutes which can lend at relatively lesser rates of interest. These businesses are very small and unprofitable over the time even though the rates of returns are exceptionally high.

Providing capital and opportunities to poor to start their business is not the solution to their improvement. Even after such provisions they will engage in the enterprises which rapidly stagnate over the time.

In order to come out of such stagnation they will need to fill that huge gap capital to incorporate production technologies which is impossible without the involvement of anti-poverty policies which will create opportunities and involvement of big formal institutes to provide no risk capital.    

“The idea of the entrepreneurial poor is helping to secure a place within the overall anti-poverty policy disclosure where big business and high finance feel comfortable getting involved.”

C. K Prahlad, taken from the book Poor Economics by Abhijit Banerjee and Esther Dulfo

Poor entrepreneurs have less risk-taking ability, no to less business connections, no credit/ loan capability when compared to their rich entrepreneur counterparts. They have to fill that huge gap of up-front capital which could have brought new production technology, employed more skilled labor. Filling this high capital gap is impossible for poor entrepreneurs. That is exactly why a smart, ingenuous street vendor even while having the best and the original ideas cannot expand his/ her business into big industries, companies and malls.

When we are understanding that poor enterprises rarely promote multiple employment/ connected employments, we should understand that supporting the poor entrepreneurship won’t drastically improve the employment rates of the nation, especially the poor nations. This is also why creation of good jobs is very important.

References:

  1. Poor Economics – rethinking poverty and the ways to end it by Abhijit Banerjee and Esther Duflo
  2. MIT OpenCourseWare – 22. Entrepreneurs and workers – Lecture by Abhijit Banerjee
  3. 106 Must-Know Startup Statistics for 2023
  4. 90% Of Startups Fail: Here’s What You Need To Know About The 10%
  5. News reference – Sifting through sludge for a sprinkle of gold – The Times of India