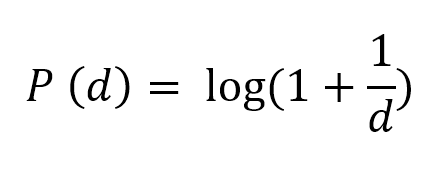Tag: data

Alan Turing’s world famous paper on future of human-like thinking ability in machines

The holy doubt – “Can machines think?”

We all know how modern machines/ computers have great abilities to make systematic thinking and take decisions accordingly; this is obviously attributed to the very programming embedded into them by us human beings. Many breakthroughs in storage capacities of computers, size of computers, efficiency of these machines, computation capabilities, evolution of programing languages, intersection of neuroscience and computer science, accessibility of these highly powerful machines to masses have shown world that such machines can do amazing marvels.

You know where I am going with this. Not mentioning Artificial Intelligence in these breakthroughs would be a straight crime. AI has unlocked a totally different capability in computing for which some are optimistic and some are fearful. In a crude sense, how AI stands out from other concepts of computing is its ability to change it programming to achieve given goal. This concept is very normal even for today’s child.

But, would you be open to such self-programming machine 75 years ago? A time when there were only mechanical calculators, electronic computers were in their infancy and were created only for certain restricted problem solving and number crunching. Even the experts of those times found this idea foolish because of the practical limitations of those times. How could a machine think like a human being when for doing some mechanical number crunching it takes such many resources, doesn’t have its own consciousness, its own soul, has no emotions to react to given stimuli? In simple words “thinking” is somehow associated as a special ability humans got because of the soul they have, the conscience they have (granted by nature, the Creator, the Almighty, the God or whatever but some higher power)

It is our tendency as human beings to have this notion of being superior species amongst all which brings in the confidence that machines cannot think. That is why this idea seemed foolish, but now we are comfortable (to some extent but not completely) with the idea of thinking machines.     

Alan Turing – a British mathematician, the code breaker of Enigma, the man who made Britain remain strategically resilient in World War 2, the Father of theoretical computer science wrote a paper which laid down the blueprint of what the future with AI would look like. For the times when this paper was published all the ideas were seemingly imaginary, impractical, and totally impossible to bring into the reality. But as the times changed, Alan’s ideas have become more and more important for the times in which we are living in and the coming future of Artificial Intelligence.

Weirdly enough, this paper which laid the foundations of artificial intelligence – thinking machines was published in journal of psychology and philosophy called “Mind”.

The world-famous concept of ‘Turing Test’ is explained by Alan in this very paper. He called this test as a game – an “Imitation Game”.

The paper reflects the genius of Alan Turing and how he had the foresight of the future – the future with thinking machine. After reading this paper you will appreciate why and how Alan was able to exactly point out every problem that would rise in future and their solutions. He was only limited by the advancements not happened in his time.

The Imitation Game   

Alan posed a simple question in this paper –

Can machines think?

The answer today (even after 75 years) is of course a straight “NO”. (Deep down we are realizing that even though machines can’t think they are way closer to copying the actions involved in thinking or “imitating” a thinking living thing)

The genius of Alan Turing was to pose practicality to find the answers to this question. He created very logical arguments in this paper where he used the technique of proof by contradiction to prove the feasibility of creating such ‘thinking machine’. The AI which has evolved today is the very result of following Alan’s blueprint for making thinking machines.

The famous Turing Test – the Imitation game is a game where an interrogator has to tell the difference between a machine and a human being by the responses they give to his/her questions.

The machine is not expected to think like humans but at least imitate them. The responses may feel completely human but it is not a condition or compulsion that machine should exactly think like a person. This practicality introduced by Alan and his arguments built upon this idea shows what are our limitations when we are actually thinking or making any decisions. This paper will change and also challenge the way we think or do anything. This paper might humble you if you think that we are superior beings because we can think and have/ express emotions. (Trust me you would also question ‘What is love?’ if love was your next answer to justify our superiority after reading this paper but that is not what Alan was focusing when he wrote this paper.)

The idea is not about creating an artificial replica of human, it is to create a machine which would respond just like humans do, the goal is to make their responses indistinguishable from ‘real’ human beings.

There are hundreds of simplified explanations on Turing test (ask Chat GPT if you want) which Alan has discussed in this paper but that is not my interest of discussion hereon.

I will be focusing only on the arguments made by Alan to prove why it is completely practical to create human-like thinking machines. My intent in doing so is that to show how we as humans can also be challenged by our practical limitations. These arguments also show a way to humans where they will get overpowered/ surpassed by AI. This does not mean that AI will eradicate humanity, rather it shows new pathways in which humanity would evolve. So, for me the arguments end on an optimistic note. Surely AI will take over the things which make us who we are but it will also push us into some completely unconventional pathways of rediscovery as the smart species.

The way in which Alan intended the Imitation game was the mode of question-answers – an interview. You would question why didn’t he think of a challenge where exact human like machine need to be created – that would be more challenging for the machines. I think, the idea behind rejecting the necessity for a machine to be in human form is like this-

The creation of human body is very similar to cloning a human body or augmenting the human parts to a mechanical skeleton. What is more difficult is to impart the consciousness and the awareness which is (supposedly) responsible to impart thinking in humans. So, even if a fully developed machine exactly looking like human being is in front of you and you are unable to tell that it is a machine, the moment that human-like machine would start expressing its thoughts everything would be easily given away.

In simple words, Alan was confident that the biological marvels, genetic engineering, cell engineering would easily take us to the physical replication of human form. What would be difficult is to create a set of logics (or self-thinking mechanism) which would demonstrate human like (thinking) capabilities. And such abilities can easily be checked by mere one on one conversation. Such was the genius of Alan Turing to bring such complexities using this simple experiment of Imitation Game.

We as human beings have certain insights, intuitions (I don’t want to use this word but don’t have any alternative word) which gives away if it is a machine or a human.

What Alan did masterfully and why he deserves full credit is that he pointed out the factors which can make machines respond and ‘think’ more like humans. While creating the confusions about the nature of human mind, consciousness, awareness, thoughts and their limitations and ambiguity, Alan also gave the possible arguments to solve these confusions.

Alan proves that human-like thinking machines can be created and he proves this by contradiction of the objections raised against this idea. I am diving deep into these objections hereon:

1. The theological objection

The rigor that Alan used to prove his point deserves appreciation. Despite being a logical thinker and mathematician, he cared to answer the religious point of view, he wanted no stone left unturned while making an argument.

Alan aggressively (verbally) hammered the idea of God’s exclusivity to grant the immortal soul to only humans, the soul responsible to make humans think. Alan says that if soul is the reason, then animals have souls too. The true comparison then should be between living and nonliving things to support the point that machines cannot think. It is because they are nonliving things they have no soul so they cannot think.

But if the great almighty can give soul to an animal, then why this omnipotent God decided to not give same souls to the machines? Alan knew that any blind theologian would find a contrived argument to prove this idea but he clarifies his point by presenting the historical mistakes religious institutes committed because the truth was hard to swallow. Alan gives the examples of Galileo who presented that earth was not the center of the universe, against the ideas of Church. Later church was proved wrong.

So, even if the religious arguments may seem easy to understand, easy to ‘swallow’ but if they are not fitting in the logic, it makes no sense to take them forward. The theological inconsistency ‘As machines have no soul granted by the God, they cannot think like humans’ which Alan pointed out  was totally false. He justifies this point using the logic of God remaining the ultimate creator.

Alan explained that if we are stealing the powers of God to create a human-like thinking ‘thing’ its not a crime or a blasphemy. Does procreating and making children “to whom also God grants the soul for thinking” mean crime? In similar spirit ‘machines’ – thinking machines are our children whom to God should bless with his powers.    

“In attempting to construct such machines we should not be irreverently usurping His power of creating souls, any more than we are in the procreation of children: rather we are, in either case, instruments of His will providing mansions for the souls that He creates.”

No doubt he would also have been a great priest if he had thought of changing his career to theology.

2. The ‘Heads in the Sand’ objection

Alan gives worst case scenarios on the superiority of human species out of all species. What if we are “the superior” species? If that is true then there is no reason to worry about thinking machines, they won’t surpass us.

But what if what we know is wrong? We have been proven wrong many times in history. What if we are not the superior species? Then there is no sense in blindly believing that we are superior. Rather this illusion of superiority steels us from the chances to fight the battle of superiority.

So, in either case, we cannot run out of the fate of thinking machines Vs humans. We may fake it, run from it, hide it from rest of the population but it is not in our favor if we do so.

“We like to believe that Man is in some subtle way superior to the rest of creation. It is best if he can be shown to be necessarily superior, for then there is no danger of him losing his commanding position.”

3. The Mathematical Objection

Very beautifully Alan brought the Gödel’s incompleteness theorem to prove his mathematical argument. According to Gödel’s incompleteness theorem, if we start to prove every mathematical argument there exists in the universe, we end up into some arguments for which there exists no proof. In order to ensure that the whole mathematical system remains stable, consistent on logic one has to accept those arguments true. So, once such logically unprovable but true in existent reality statements are found in nature they create a new system of mathematical understanding.

In simple words, every mathematically logical system is inconsistent in the end, in order to remove that inconsistency a new rule must be accepted which create a new system of mathematics. (Which again would be inconsistent)

Further oversimplification goes like this,

A farmer wouldn’t know how to make a shoe. So, he would need knowledge of a cobbler. A cobbler wouldn’t know how to make metal tools, so he would need help of blacksmiths. Even if they have each other’s knowledge, skills they must accept certain thumb rules passed down from their ancestors (which are always true but unprovable) to master each other’s skills.  

So, even if you are creating a thinking machine based on purely mathematical system the mere limitation of mathematics will stop it from overpowering, surpassing humans.

This also does not mean that thinking machines are defeat-able. A machine with one mathematical system in totally different domain could support this logically inconsistent system just like the villagers with different professions.

Alan Turing’s doctoral thesis contains the ideas of Gödel’s Incompleteness theorem so it is a joy to read these arguments in this paper. They are well formed and super-intelligent.

(If you are really interested what this argument means, you can research the efforts that went into proving Fermat’s last theorem. A new field of mathematics had to be created to prove this simple to explain but difficult to prove mathematical theorem.)

There will always be something cleverer than the existing one – for humans and for thinking machines too.

“There would be no question of triumphing simultaneously over all machines. In, short, then, there might be men cleverer than any given machine, but then again there might be other machines cleverer again, and so on.”

4. The argument from Consciousness

Even if the machine is feeling and thinking exactly like a human being, how could the “real humans” know that it does so? – Alan’s new argument.

“The only way to know that a man thinks, is to be that particular man. It is in fact the solipsistic point of view. It may be the most logical view to hold but it makes communication of ideas difficult.”

Communication between machines and the humans and its quality would be key proof to understand whether the machine thinks like human beings or not. Even if the machine is really thinking exactly like humans, it is futile if it cannot communicate so to humans.

(That is exactly why The Turing test with mere typed communication is more than enough to check the thinking ability of machines.)

It is the great philosophical mind of Alan to use the limitations of Solipsism to justify his point. According to solipsism all the world exists in the mind of the person because if the person dies then it doesn’t matter if world is there or not.

The key limitation of solipsism is that your survival is not directly connected to your mere thinking. If I think ‘I am dead’ that does not immediately kill me. If I think that I have eaten a lot without actually eating anything, that doesn’t end my hunger in ‘reality’. So, reality is not only your mind.

Also, solipsism fails to answer the common experiences we have in a group. If my mind is my world, I can create any rules for my world and things would always go as I desire. But that doesn’t happen in reality. There are certain ways, truths which are common to all of us that is why our world is not just our mind, rather it may be a shared world. You alone are not the representation of whole reality.

So, even if we accept that the machine ‘inwardly’ thinks like human being, it has to share some common truths to the interrogator to prove its humanly ways of thinking.

“I do not wish to give the impression that I think there is no mystery about consciousness. There is for instance, something of a paradox connected with any attempt to localize it. But I do not think these mysteries necessarily need to be solved before we can answer the question…. (the question – can machines think? Can they at least imitate humans? – the Imitation Game)”

5. Argument from various disabilities

Alan is challenging the idea that even if machines are successful in thinking exactly like humans, they won’t be able to do certain things which humans can do better.

It’s like a human saying to a thinking machine –

“You machines can think like us but can you enjoy literature and poetry like we humans do, can you have sex just like humans do, enjoy it and procreate just like we (human) do? This is exactly why your thinking is not a human thinking.”

The key point Alan is trying to prove is that people always need a justification of given machine’s ability (through its ways of working, maybe its architecture, its technology, its components, its sensors) to prove that certain capability of the machine. When we are showing these justifications, we are also telling people indirectly what it cannot do thereby its disabilities. One ability would point to other disability.

People do not accept black box models in order to justify ability of the machine.

“Possibly a machine might be made to enjoy this delicious dish, but any attempt to make one do so would be idiotic. What is important about this disability is that it contributes to some of the other disabilities.”

In same fashion one argument is that even if machine could think like humans, it is difficult to have its own opinion. Alan strikes that too.

“The claim that a machine cannot be the subject if its own thought can of course only be answered if it can be shown that the machine has some thought with some subject matter.”

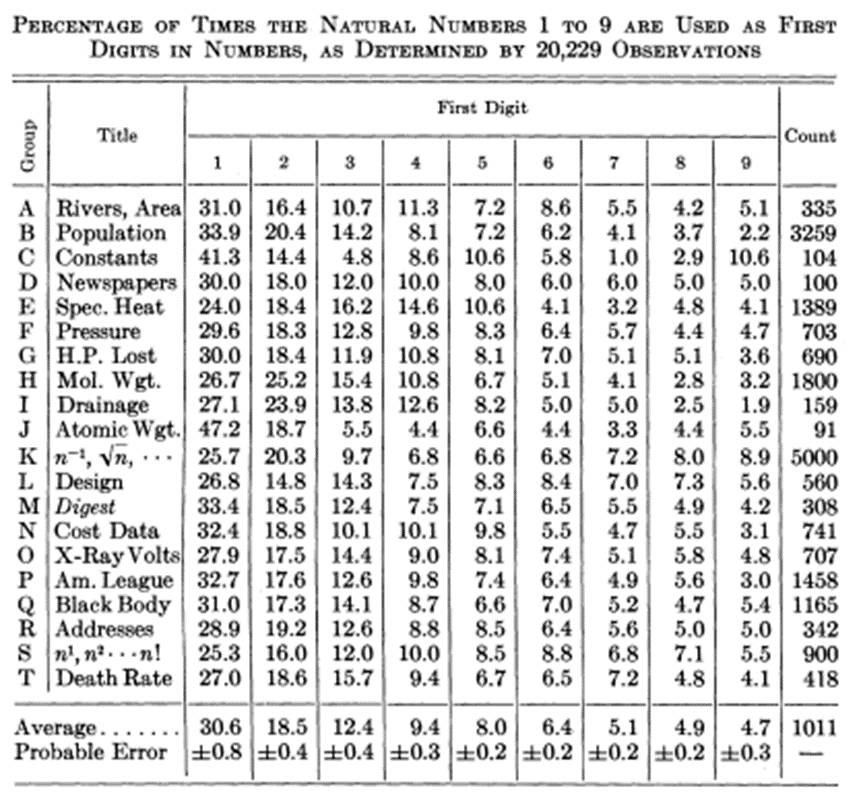
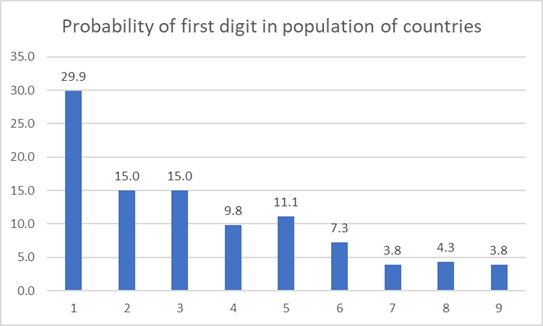
The key disability which was preventing Alan from creating a working thinking machine was the enormous storage space. You will appreciate this point today because you know how drastically storage capabilities have improved over the time. These improvements in storage created the AI we see today, although processing power is also on factor and there are other factors too but it boils down to the ability to simultaneously handle lot and lots of data.

Alan had this mathematical insight that once the storage ability is expanded enough the thinking machines is a practical reality. (Now researchers are not only working on to further improve storage capability but special efforts are also taken to effectively compress data. Ask Chat GPT about the Hutter Prize)

So, Alan makes a point that having variety of opinions in order to ‘think for itself’ machines don’t need logic, they need enough storage space just to process them simultaneously to create a new thought. In terms of humans, the more information and logic you can handle the crisper your understanding are. Same would be the case for thinking machines.

“The criticism that a machine cannot have much diversity of behavior is just a way of saying that it cannot have much storage capacity. “

6. Lady Lovelace’s Objection

Charles Babbage was the first person to technically create calculator with memory – a programmable computer which they called Analytical Engine. Even though he knew how the Analytical Engine works Ada Lovelace created programs and published them to the masses to prove the effectiveness of the Analytical Engine. She was the first programmer of computer.   

Lady Lovelace’s key argument is based on the idea that the computer thereby a thinking machine cannot think for itself because it can only use what we have provided it. As we have provided whatever we know and have it cannot think outside of that information and generate new understandings, The machines cannot think “originally”.

Alan strikes down this argument easily using the idea of enough storage space. If the machine can store large enough data and instructions then it can create new inferences, original inference.

“Who can be certain that ‘original work’ that he has done was not simply growth of the seed planted in him by teaching, or the effect of following well-known general principles.”

Alan questioned the very nature of originality. Only a genius can do this in my opinion. Alan showed the world that the things which we call original are inspired, copied from something already existent. It is just matter of how unknown we are to this new thing.

He builds further upon that saying that if machines can think originally then they should surprise us. That is reality. Machines do surprise us by using unconventional approaches to our daily tasks. 

Alan links new argument for further justification, if machines can think originally then they can surprise us. In order for us to not get surprised we must get immediate understanding of what machine presents which never happens when such events happen. So, machines can think originally and can surprise us.

“The view that machines cannot give rise to surprises is due, I believe, to a fallacy to which philosophers and mathematicians are particularly subject, This is the assumption that as soon as a fact is presented to a mind all consequences of that fact spring into the mind simultaneously with it.”

What a brilliant argument!

7. Argument from Continuity

“The nervous system is certainly not a discrete-state machine. A small error in the information about the size of a nervous impulse impinging on a neuron, may make a large difference to the size of the outgoing impulse. It may be argued that, this being so, one cannot expect to be able to mimic the behavior of the nervous system with a discrete-state system.”

Alan talks about an attempt to create thinking machines by mimicking nervous system which is a continuous system. A system which works in wave, signals (analog) and not in ones and zeros (discrete).

Alan says that even if we use such analog system in Turing test, the outputs it would give would be probabilistic instead of definite. This will actually make the interrogator difficult to distinguish human response from the machine one. Humans would be more frequently unsure and will give such probabilistic answers more frequently.  

8. The argument from Informality of Behavior

“If each man had a definite set of rules of conduct by which be regulated his life, he would be no better than a machine. But there are not such rules, so men cannot be machines.”

The idea that machines work on certain defined rule even if they can alter their own program by themselves in order to think like humans, it feels obvious that they will be more formal and stuck to their rules while responding. This formality would give away their non-human nature.

Alan questions the very nature of what is means to have laws in a logical setup. Taking support from the Gödel’s Incompleteness theorem, not even single system – single logical system can confidently remain purely on its laws. It would assume some arbitrary point to make some sense out of given data even if it is using some mathematical frameworks. (Remember the simulations where you put garbage in and the simulations runs perfectly giving garbage out. But you know its garbage because you have certain test to judge the output with reality which are objective.)

There is no such objectivity to judge informality of a system – the word and logic itself says it all. Our search for formal laws would never end and this will always keep on creating new laws and new inconsistencies and informalities. There is no end.    

“We cannot so easily convince ourselves of the absence of complete laws of behavior as of complete rules of conduct. The only way we know of for finding such laws is scientific observation, and we certainly know of no circumstances under which we could say, ‘We have searched enough. There are no such laws.’”

9. The Argument from Extra-sensory Perception

“The idea that our bodies move simply according to the known laws of physics, together with some others not yet discovered but somewhat similar, would be one of the first to go. This argument is to my mind quite a strong one. One can say in reply that many scientific theories seem to remain in practice, in spite of clashing with ESP; that in fact once can get along very nicely if one forgets about it.”

Again, Alan left no stone unturned. He made sure that even the pseudo-science fails to support the idea that machines cannot think like humans.

He explains that even if the human competing against the machine mimicking humans has telepathic abilities to know states of the machine or even the interrogator, it would actually confuse the interrogator. The only thing such telepathic person can do differently is to under-perform intentionally which again would confuse the interrogator.

The idea is that even when we are not sure of how such supernatural things works our current understanding of things and their workings are just fine. The supernatural things are not interfering in our formal understanding of nature and reality.

The implications of Alan Turing’s Paper on Computing Machinery and Intelligence

All the ideas explained by Alan in this paper are responsible for the modern technologies like efficient data storage, data compression, artificial neural networks, self-programming machines, black box models, machine learning algorithms, iterative learning, data storage, manipulation thereby data science, analog computing, self-learning, supervised learning algorithms, Generative Pre-Trained Transformers (GPTs) and what not.

This paper is holy grail for not only modern computer science but also for the literature and popular culture. Once you appreciate the ideas in this paper you will be able to see the traces of these ideas across all the modern science fiction we are consuming all the time.

Alan created practical ideas which were possible to implement in future based on the coming technological revolutions he foresaw. He logically knew that it is possible but the genius of him was to lay the practical foundation of what and how it needs to be done which is guiding our and will guide future generations.

Conclusion

What is there for humans if machines start thinking like humans?

For this, I will address each argument posed by Alan

1.  The theological objection

God will actually bless us because we extended his (or her I don’t know) powers to create something like his own creation through thinking machines.

2. The ‘Heads in the Sand’ objection

Even if thinking machines surpass us, we have to live with it and create our new ecosystem to ensure our survival. Even though for given times we are superior species, other species are existing with us in the same time with their special abilities. There is no running away from any possible outcome of this scenario.

3. The Mathematical Objection

The mathematics itself restricts a single machine from knowing everything. So even if multiple machines come together to create superior understandings same would happen for humans. There will always be this race of superiority, sometimes machines will lead sometimes humans will lead. There is no conclusion to this race as far as the inherent flaw of mathematics goes.

4. The argument from Consciousness

A machine has to be the communicator of its human thinking, it cannot remain in the dark abyss of self-cognizance and remain away from humans. If a machine starts thinking like humans, we all would definitely know about it. A machine has to communicate its ability of awareness to, it will a surprise but a very short lived one.

5. Argument from various disabilities

If we don’t know how machines think like human that would not prevent them from thinking like humans. We have to accept the black boxes through which machines would think like humans. That is the only sane way out. We humans too are filled with disabilities but they are not directly linked to the ways we are able to think.

6.  Lady Lovelace’s Objection

Machines will surprise us, they can also create original ideas, because what we call original is something that lies out of the limits of our current thinking. Rather it is an optimistic idea that if machines could think like humans do then they may give us totally new ideas for new discoveries, breakthroughs.

7. Argument from Continuity

Continuous thinking machine or discrete thinking machine both can confuse humans if they achieve their thinking potentials. So, there is no point in creating an analogue thinker to beat digital thinker. We ourselves are an analogue thinker.

8. The argument from Informality of Behavior

No system will have all laws already established, the system has to keep on creating new laws to justify new events, outliers. The process is never-ending. So even if machines surpass in human thinking we too have the advantage of informality to make the next move.

9. The Argument from Extra-sensory Perception

Even if the supernatural abilities are proven be existent, they will have less to no contribution in the thinking abilities of machines. So, if you are a telepathic reader a human like thinking machine can fool you without exposing its real machine identity.

Going through all this you will appreciate how limited our human thinking is. There is no doubt that there will be a time when machines would be able to think just like humans do but that should not be a negative aspect. There will be practical limitations to a human-like thinking machine too. So, the game would never be single sided. This should push humanity on a completely new path of evolution. That is also how we have become the humans we are today.

Further references for reading:

1. A. M. TURING, I.—COMPUTING MACHINERY AND INTELLIGENCE, Mind, Volume LIX, Issue 236, October 1950, Pages 433–460, https://doi.org/10.1093/mind/LIX.236.433
2. Understanding the true nature of Mathematics- Gödel’s Incompleteness Theorem
3. Questioning Our Consciousness – Solipsism