Game Theory – Minding our decisions

Human relationships are more of multiple complex interactions. The interactions with living or non-living bodies create some actions and these actions have some favorable or unfavorable outcomes. The word “relationship” here is not used just as in parents, siblings, in-laws or acquaintances but as a connection to everything around us, mostly living things. The awareness of our actions and their consequences- that visualization of cascade is one of the major parts of our knowledge building, relationship development, behavior management, personality development.

As a sane creature (most of the time) we try to calculate the consequences of our actions, have a thought about it and then decide our strategy while acting on something. This is what some people call the motivation or habit or trait of that person, that character. Important thing to understand is that every action always has multiple outcomes which brings the complexity in the expected outcomes of the scenarios. Different people have different motivations/ habits/ traits so they react and decide in different way adding further complexity to the scenario.

Take a simple example:

Many a times when you are trying to call your friend this happens. You call him, his phone rings but he doesn’t pick up. Then he notices the missed call and tries to call you while you are already calling him. The call remains engaged from both sides. Then you both wait for exactly the same time oping that the one on other side will call.

This goes for some time, and after some trial and error your call gets connected.

What should be an optimal strategy for such simple scenarios?

There is a rigorous field of mathematics and economics (not limited to these only and rather a wide field) which can deal with such problems and far more complex problems in our day-to-day interactions.

“Game theory is the study of mathematical models of strategic interactions among rational agents.”

 Simply put, game theory can give answers to have the best strategy for the interactions which can be business interactions, economical interactions, national interactions, war strategies or competitor strategies. The idea of Game theory was developed by famous mathematician Jon von Neumann and economist Osker Morgenstern. Let us dive in deeper.

Basic Definitions in Game Theory

Game– A game is any situation in which players (the participants- the agents) make strategic decisions—i.e., decisions that take into account each other’s actions and responses.

Agents– The participants, the players of the game.

Rational Agents– This is the most important idea in Game theory where the rationality of agent is the idea of welfare of the agent. The agent will always try to achieve its own welfare. In economics this is known as maximizing the utility.

A rational agent always tries to maximize its utility.

Strategy– Rule or plan of action for playing the game.

Payoff/ Outcome– The value of utility, extent of welfare from certain strategy. It is numerical, quantified measure of the benefit from a strategy.

Optimal Strategy– A strategy which maximizes the utility of an agent.

Please note that the clear definition of utility, rational agent, optimal strategy defines the boundaries of the problems in Game theory thereby making it mold-able into the mathematical models (although mathematical models can consider the factors beyond boundaries but it will make the problem unnecessarily complicated). Mathematical models as in the mathematical equations which can be solved using general techniques to get the maximized outcome for the agents.

Please note that the word “Game” in game theory can be any situation which requires strategic decision making involving more than one agent. The game can be simple like Stone-Paper-Scissors, Tic-Tac-Toe or a Chess game to more complex game like launching a new smart phone in the market or taking over a company or setting up a war with a nation or even winning the general elections of the country.

The Prisoner’s Dilemma

The Prisoner’s Dilemma is the most common and famous example to understand the basics of Game Theory. Consider a scenario:

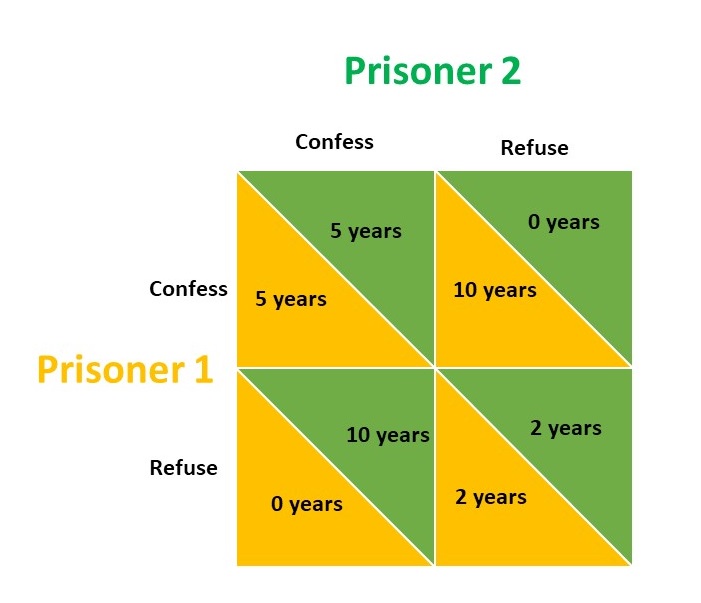
Two persons are arrested by Police under the crime of armed robbery. The Police know that they have committed this robbery together but they don’t have enough proof to justify that. They can only charge the persons under the theft of the car used for robbery due to lack of evidences. Police think that if both persons confess the armed robbery, then they can easily jail them under the proper charges of armed robbery. So, they lock each of them in separate cell and ask them to either confess or deny the crime.

The police inspector tells each one of them separately in their cell the following:

If only one of you confesses the crime and the other doesn’t, then the one who confesses will be freed but the another one refusing will be sentenced for 10 years. If you both confess, you’ll each get 5 years. If neither of you confess, then you’ll each get two years for the car theft.

Now, if we see the overall scenario, the best thing for both the prisoners is to deny the crime and set themselves free at first, but if you think properly of all the consequences and the information available to both the prisoners, that is not the best strategy.

The common information of three possible cases given to both the prisoners by the policeman is known as Information Set in Game theory.

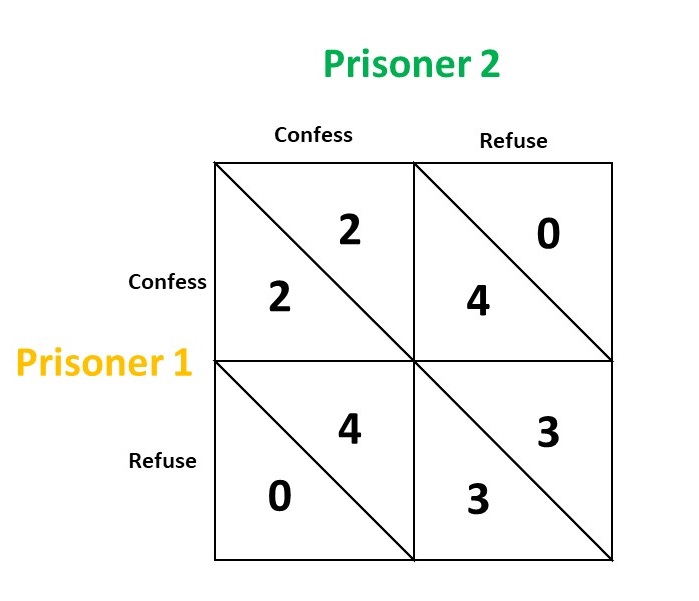
So, the outcomes of such scenario can be arranged in a table to form a matrix which is also known as the Normal Form in game theory.

If we assign a number to each the payoff of each strategy,

1. 0 for the worst case- 10 years of jail
2. 2 for 5 years of jail
3. 3 for 2 years of jail
4. 4 for becoming free, no jail

then the normal form can be given as follows:

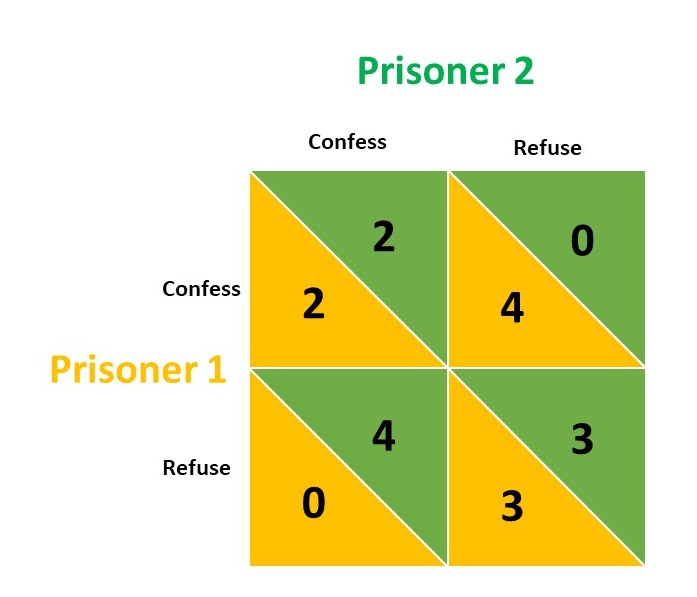
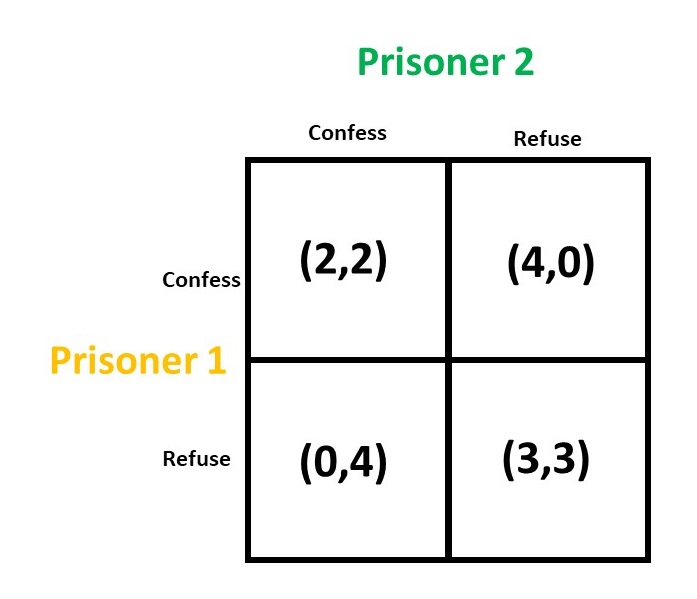
 It becomes very easy to see as an agent of this game- the prisoner will try to maximize his utility by refusing the crime thereby setting him free. But the catch here is that he doesn’t know what another prisoner has done- whether he confessed or refused the crime.

Now, we need to understand that the final outcome is not dependent on only one prisoner decision. Hence, the decision making of second prisoner will affect the decision making of first prisoner. Let us see from the perspective of Prisoner 1:

1. Refusing should be the best idea, but if Prisoner 1 refuses and the Prisoner 2 confesses then it will lead to 10 years of imprisonment (zero utility) for Player 1 more risky operation as he is not sure about Prisoner 2’s decision.
2. If Prisoner 1 confesses the crime, then there are two possibilities:
   • Prisoner 2 also confesses thereby both will get 5 years of sentence (utility of two)
   • Prisoner 2 denies thereby prisoner 1 getting freed and Prisoner 2 gets sentenced for 10 years (utility of 4 for prisoner 1 and zero for prisoner 2)

 So, confessing becomes the best strategy for both the prisoners when they are in an isolated cell.

Which is why the optimal strategy for both the prisoners of this game is to confess. In any possible decision by another prisoner, it will give the best possible outcome.

The one thing important to notice here is that they both could have refused simultaneously. Because, if they both refuse it would have maximized the utility of both (2 years of jail for both, utility of 3 for both). The thing is that the risk associated with refusing is more than the risk associated with confessing. Thus, even if the utility is highest in some cases the interaction of other players forces a player to choose optimal strategy which will yield the best irrespective of other players decisions.

The Nash Equilibrium

Mathematician John Nash took the Game theory developed by Neumann and Morgenstern and provided mathematical background for finding the strategy where the solution will be optimal irrespective of the decision made by the other players. For that we need to understand the two types of games – Cooperative and non-cooperative games

If the prisoners in above examples are supposed to have a word with each other before presenting their opinion to the police they surely would have understood that refusing will benefit them both, which when exploited is a collusion – a foul play, here in the prisoner’s game it is exploited.

But as we know in reality, even if they are given a meet to discuss before presenting their opinion there is still that risk of changing the statement at the last minute (!) thereby making the game a non-cooperative game. Nash Equilibrium exists in such non-cooperative games.

A cooperative game represents the game where players agree to work towards a common goal. It’s like splitting your restaurant bill with your friends. Here the main focus remains on the contribution from each player, like Coalition of Countries to reduce carbon footprint, to stop Global Warming. Shapley value is used in cooperative games instead of Nash Equilibrium. Shapley value distributes the payoff based on the contribution a player makes in the game.

Shapley value simply decides the fairness of payoff for each player in cooperative game whereas Nash equilibrium decides the best decision to maximize the payoff in a non-cooperative game.   

“In non-cooperative games there exists an equilibrium at which no side has any rational incentive to change the chosen strategy even after running through all the choices available to the opponent”

In short, Nash Equilibrium is like a law which needs no punishment to enforce to the rational people, because the people understand that breaking that law will not benefit them.

It is like following a traffic signal properly. If all will rush at the crossing all will be late in their journey maybe possible deaths due to accidents. Following the time-based signal will give opportunity to everyone, thereby zeroing the risk of accidents and saving the travel time. (And still some people break the signal, hence the word “rational agent” is of highest importance in Game theory!)

John Nash – a mathematician received Nobel Prize in economics for his work of Nash Equilibrium. The development of mathematical tools further for game theory revolutionized the economics. The movie on his life called “A Beautiful Mind” depicts his original thought process in a beautiful way.

Assumptions of Game Theory

1. All players are utility maximizing rational agents that have full information about the games, rules and the outcomes/ payoffs. (So that the mathematical models will fit)
2. Players are not allowed to communicate – no coalition in a bad way – no collusion- no foul play (hence the reason Governments also establish anti-collusion, antitrust laws, anti-monopoly laws in real world)
3. Possible outcomes are known in advance and cannot be changed (Deterministic models, hence the reason many equity traders try to find some trends in the equity indices based on certain assumptions)
4. The number of players can be infinite but most of the games will contextualize in terms of two players only (thereby simplifying the model).

Strategies of Game theory

1. Pure and mixed strategies:
   • PURE- Players follow same strategy in the game- All the companies may increase the product prices of their products to increase the profit. (Actually, it not that simple)
   • MIXED- Different players follow different strategy in the game. (One company will try to sell less but expensive units, the another one will try to market the best-in-class after-sales services) 
2. Dominant and dominated strategies:
   • A dominant strategy leads to the best of all alternative payoffs
   • a dominated strategy leads to the worst of all alternative payoffs
   • Say, there are two companies A and B both have two products – consumer and professional. The market has 80 % of consumers and 20 % of professionals. What can A and B do.
   • Company A and B both will enter both the consumer and professional market hence each will get 50% of the share from total market (half of consumer i.e., 40% consumer and half of professional i.e., 10% of professional market to each company), thereby maximizing the utility which is Dominant Strategy
   • Company A and B both will enter only professional market (which is already 20% of whole market- smaller market share) so both will get only 10% each of the total market thereby getting the least amount of market share which is Dominated strategy
   • Only company A can enter in consumer market and company B can enter professional market thus one will get complete consumer market and the another will get complete professional market. Reverse is also possible here.
   • The example i) here is called as Strictly Dominant Strategy, example ii) is called as Strictly Dominated strategy.
3. Maximin strategy – A strategy which will maximize the profit, the utility in the game
4. Minimax strategy- A strategy which will minimize the loss in the game

Game Theory for Life- The Concept of Finite and Infinite Game

The applications of Game theory are uncountable in real world. The complexity of real-life problems projects an impression as if Game theory has just started developing like a new born baby. The problems Game theory can solve and the promises it provides can add great value to humanity.

In order to understand the depths of the contributions of the Game Theory, we must understand the idea of Finite and Infinite Game.  

The finite game has known players, fixed rules, has an end point where there is one winner and there in one loser- a zero sum game. Like the game of chess, the game has two players, all the rules are fixed and cannot be changed by some external influence, either one of the kings gets the checkmate or the match becomes draw- no win or no lose- the game ends.

The infinite game is an eternal game- it goes on. The resources are infinite, the rules keep on changing, the players come and go. The infinite game is similar to what our life is. If one knows how to win an infinite game, then he/she can also win a life.

Simon Sinek has a beautiful book called “The Infinite Game” where he has explained how to win at an infinite game and thereby possibly at life. The insight from the idea of an infinite game is that the main goal of the game is to keep it playing. As the resources are infinite, players are infinite, rules are changeable- there is no endpoint for such game which will justify the worth of the winner. There is no winner.         

Most of the games in economics, finance may seem finite games for once but deep down, when explored further are the infinite games, our life is the best example of it. Simon Sinek has given many lectures, talks about the mindset for infinite game which are beautiful. They are beautiful because they reflect the philosophical nature of Game theory and its synergy to human decision making which is not rational all the times. Simon Sinek highlights on five headers while discussing the infinite games.

1. Just cause- A Specific vision for the future which is yet to exist. It is powerful enough to motivate people, make sacrifice for it.
2. Trusting teams- Creating room for improvements, improvements will lead to evolution, development. This will truly lift the human spirit. It is about the creation of psychologically safe environment where people can demonstrate who they are and improve over it to last longer in the game.
3. Worthy rival- As the game is infinite- won’t end, the rival should always inspire one to elevate the game thereby strengthening both the sides. If the rival is not strong- worthy the game will end to some part but still new player will enter and perpetuate the game, thus the sustenance demands worthy rival.
4. Existential Flexibility- Disruption for more effective development leading to evolution
5. Courage to lead- Given the uncertainty of the outcome, a risk-taking attitude for the unknown but good future dependent upon the just cause is important to live through the infinite game.

Such ideas given for the infinite game can help build better organizations, better teams, better institutions.

The Game theory itself represents an institution which has proved to become useful in not only economics but also in philosophy of humanity.

(We can deduce the optimal strategy for the engaging phone call game using Game theory. The optimal strategy is to do what both sides were doing before initiating the call. Thus, the one who tried calling first should continue calling whereas the one receiving the call should wait for the call rather than calling back! Please assume the rationality of your friend, willingness of your friend to accept the call, strong signal strength for the game!)

References and Further Readings:

1. The Infinite Game by Simon Sinek
2. Ross, Don, “Game Theory”, The Stanford Encyclopedia of Philosophy (Fall 2021 Edition), Edward N. Zalta (ed.)
3. Game Theory: Definition, Role in Economics, and Examples by investpedia.com
4. What game theory teaches us about war | Simon Sinek – TED Archive
5. The Infinite Game for New York Times
6. Strategic Dominance: A Guide to Dominant and Dominated Strategies by effectivology.com
7. Photo of Jon von Neumann from Wikimedia and www.lanl.gov
8. Photo of John Nash from Wikimedia and Peter Badge
9. Photo of Simon Sinek from Wikimedia
10. Memes from